Shripad Gade
GEM+: Scalable State-of-the-Art Private Synthetic Data with Generator Networks
Nov 12, 2025
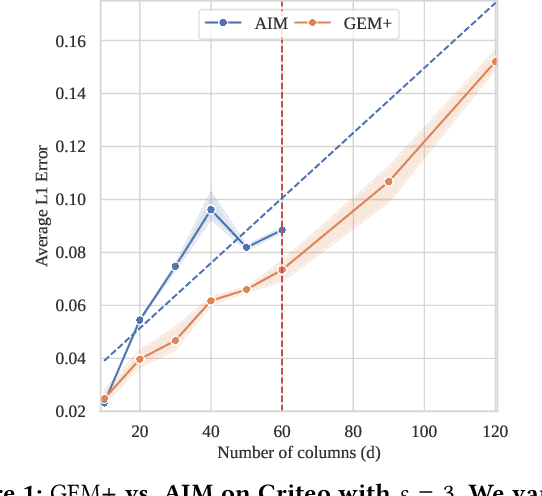
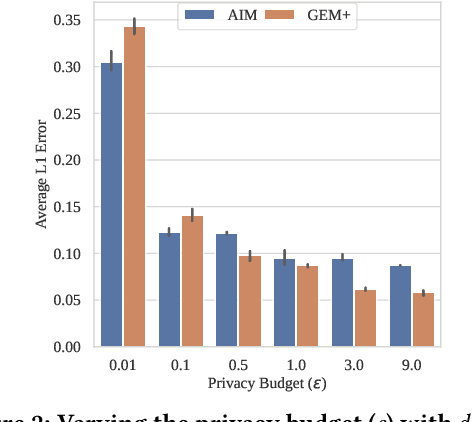

Abstract:State-of-the-art differentially private synthetic tabular data has been defined by adaptive 'select-measure-generate' frameworks, exemplified by methods like AIM. These approaches iteratively measure low-order noisy marginals and fit graphical models to produce synthetic data, enabling systematic optimisation of data quality under privacy constraints. Graphical models, however, are inefficient for high-dimensional data because they require substantial memory and must be retrained from scratch whenever the graph structure changes, leading to significant computational overhead. Recent methods, like GEM, overcome these limitations by using generator neural networks for improved scalability. However, empirical comparisons have mostly focused on small datasets, limiting real-world applicability. In this work, we introduce GEM+, which integrates AIM's adaptive measurement framework with GEM's scalable generator network. Our experiments show that GEM+ outperforms AIM in both utility and scalability, delivering state-of-the-art results while efficiently handling datasets with over a hundred columns, where AIM fails due to memory and computational overheads.
Synthetic Tabular Data: Methods, Attacks and Defenses
Jun 06, 2025Abstract:Synthetic data is often positioned as a solution to replace sensitive fixed-size datasets with a source of unlimited matching data, freed from privacy concerns. There has been much progress in synthetic data generation over the last decade, leveraging corresponding advances in machine learning and data analytics. In this survey, we cover the key developments and the main concepts in tabular synthetic data generation, including paradigms based on probabilistic graphical models and on deep learning. We provide background and motivation, before giving a technical deep-dive into the methodologies. We also address the limitations of synthetic data, by studying attacks that seek to retrieve information about the original sensitive data. Finally, we present extensions and open problems in this area.
Leveraging Vertical Public-Private Split for Improved Synthetic Data Generation
Apr 15, 2025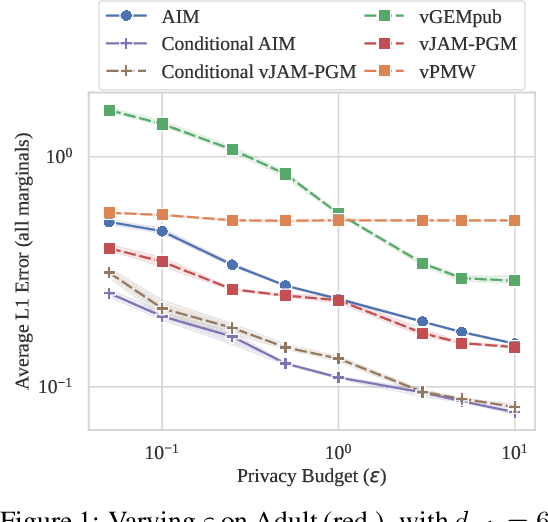


Abstract:Differentially Private Synthetic Data Generation (DP-SDG) is a key enabler of private and secure tabular-data sharing, producing artificial data that carries through the underlying statistical properties of the input data. This typically involves adding carefully calibrated statistical noise to guarantee individual privacy, at the cost of synthetic data quality. Recent literature has explored scenarios where a small amount of public data is used to help enhance the quality of synthetic data. These methods study a horizontal public-private partitioning which assumes access to a small number of public rows that can be used for model initialization, providing a small utility gain. However, realistic datasets often naturally consist of public and private attributes, making a vertical public-private partitioning relevant for practical synthetic data deployments. We propose a novel framework that adapts horizontal public-assisted methods into the vertical setting. We compare this framework against our alternative approach that uses conditional generation, highlighting initial limitations of public-data assisted methods and proposing future research directions to address these challenges.
Private Learning on Networks: Part II
Nov 05, 2017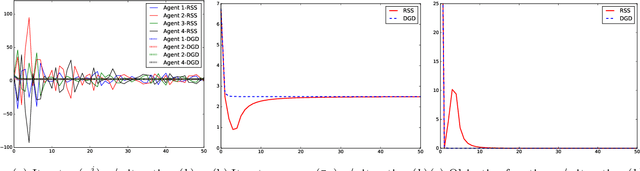

Abstract:This paper considers a distributed multi-agent optimization problem, with the global objective consisting of the sum of local objective functions of the agents. The agents solve the optimization problem using local computation and communication between adjacent agents in the network. We present two randomized iterative algorithms for distributed optimization. To improve privacy, our algorithms add "structured" randomization to the information exchanged between the agents. We prove deterministic correctness (in every execution) of the proposed algorithms despite the information being perturbed by noise with non-zero mean. We prove that a special case of a proposed algorithm (called function sharing) preserves privacy of individual polynomial objective functions under a suitable connectivity condition on the network topology.
Distributed Optimization for Client-Server Architecture with Negative Gradient Weights
Dec 19, 2016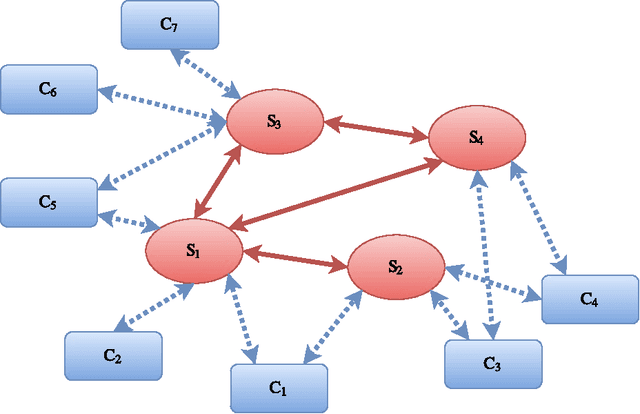
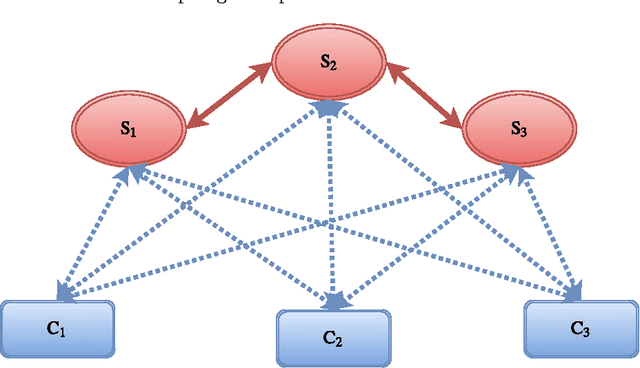
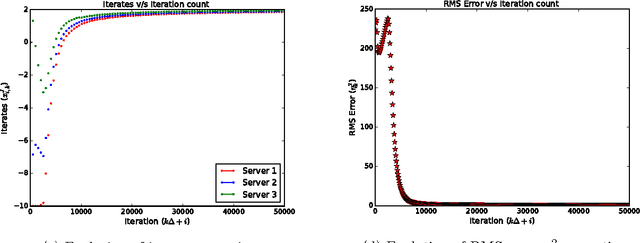
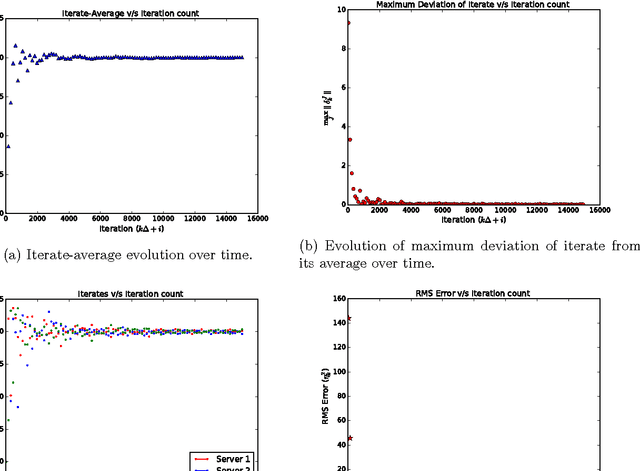
Abstract:Availability of both massive datasets and computing resources have made machine learning and predictive analytics extremely pervasive. In this work we present a synchronous algorithm and architecture for distributed optimization motivated by privacy requirements posed by applications in machine learning. We present an algorithm for the recently proposed multi-parameter-server architecture. We consider a group of parameter servers that learn a model based on randomized gradients received from clients. Clients are computational entities with private datasets (inducing a private objective function), that evaluate and upload randomized gradients to the parameter servers. The parameter servers perform model updates based on received gradients and share the model parameters with other servers. We prove that the proposed algorithm can optimize the overall objective function for a very general architecture involving $C$ clients connected to $S$ parameter servers in an arbitrary time varying topology and the parameter servers forming a connected network.
Private Learning on Networks
Dec 15, 2016



Abstract:Continual data collection and widespread deployment of machine learning algorithms, particularly the distributed variants, have raised new privacy challenges. In a distributed machine learning scenario, the dataset is stored among several machines and they solve a distributed optimization problem to collectively learn the underlying model. We present a secure multi-party computation inspired privacy preserving distributed algorithm for optimizing a convex function consisting of several possibly non-convex functions. Each individual objective function is privately stored with an agent while the agents communicate model parameters with neighbor machines connected in a network. We show that our algorithm can correctly optimize the overall objective function and learn the underlying model accurately. We further prove that under a vertex connectivity condition on the topology, our algorithm preserves privacy of individual objective functions. We establish limits on the what a coalition of adversaries can learn by observing the messages and states shared over a network.
Distributed Optimization of Convex Sum of Non-Convex Functions
Aug 18, 2016
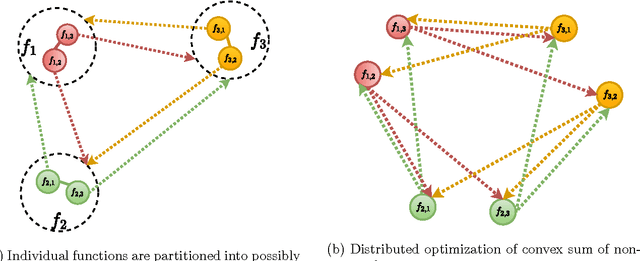
Abstract:We present a distributed solution to optimizing a convex function composed of several non-convex functions. Each non-convex function is privately stored with an agent while the agents communicate with neighbors to form a network. We show that coupled consensus and projected gradient descent algorithm proposed in [1] can optimize convex sum of non-convex functions under an additional assumption on gradient Lipschitzness. We further discuss the applications of this analysis in improving privacy in distributed optimization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge