Private Learning on Networks: Part II
Paper and Code
Nov 05, 2017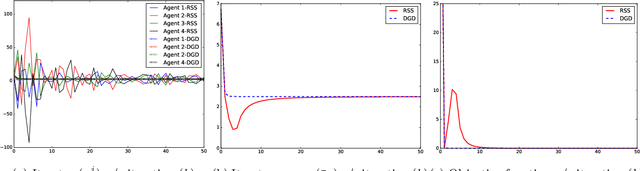

This paper considers a distributed multi-agent optimization problem, with the global objective consisting of the sum of local objective functions of the agents. The agents solve the optimization problem using local computation and communication between adjacent agents in the network. We present two randomized iterative algorithms for distributed optimization. To improve privacy, our algorithms add "structured" randomization to the information exchanged between the agents. We prove deterministic correctness (in every execution) of the proposed algorithms despite the information being perturbed by noise with non-zero mean. We prove that a special case of a proposed algorithm (called function sharing) preserves privacy of individual polynomial objective functions under a suitable connectivity condition on the network topology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge