Impact of Redundancy on Resilience in Distributed Optimization and Learning

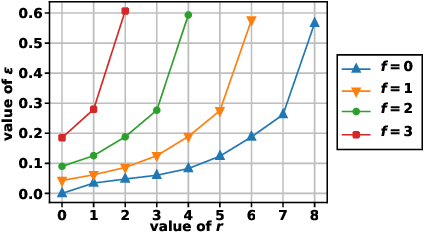
This report considers the problem of resilient distributed optimization and stochastic learning in a server-based architecture. The system comprises a server and multiple agents, where each agent has its own local cost function. The agents collaborate with the server to find a minimum of the aggregate of the local cost functions. In the context of stochastic learning, the local cost of an agent is the loss function computed over the data at that agent. In this report, we consider this problem in a system wherein some of the agents may be Byzantine faulty and some of the agents may be slow (also called stragglers). In this setting, we investigate the conditions under which it is possible to obtain an "approximate" solution to the above problem. In particular, we introduce the notion of $(f, r; \epsilon)$-resilience to characterize how well the true solution is approximated in the presence of up to $f$ Byzantine faulty agents, and up to $r$ slow agents (or stragglers) -- smaller $\epsilon$ represents a better approximation. We also introduce a measure named $(f, r; \epsilon)$-redundancy to characterize the redundancy in the cost functions of the agents. Greater redundancy allows for a better approximation when solving the problem of aggregate cost minimization. In this report, we constructively show (both theoretically and empirically) that $(f, r; \mathcal{O}(\epsilon))$-resilience can indeed be achieved in practice, given that the local cost functions are sufficiently redundant.

Byzantine Fault-Tolerant Distributed Machine Learning Using Stochastic Gradient Descent (SGD) and Norm-Based Comparative Gradient Elimination (CGE)

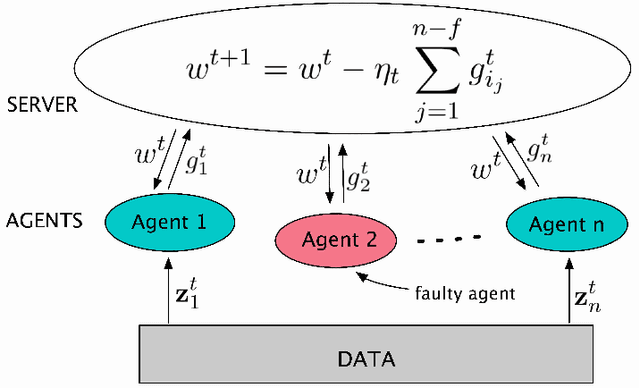
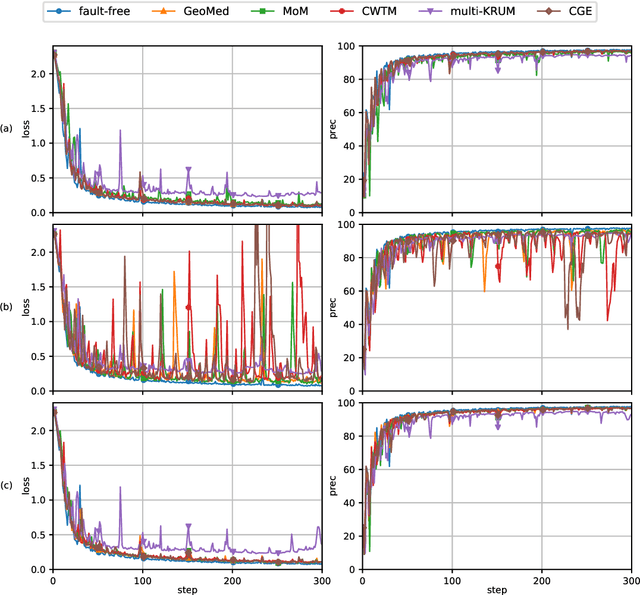
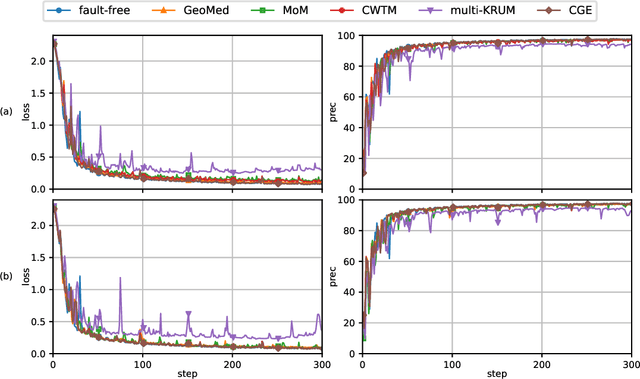
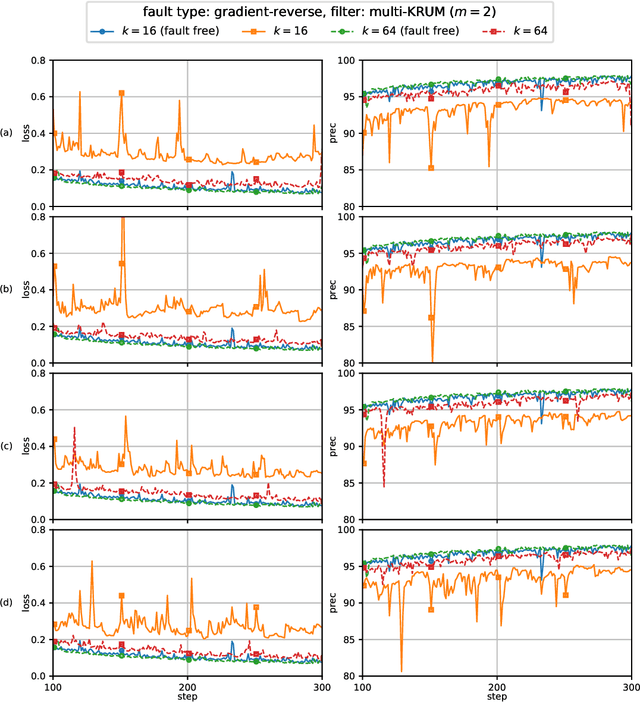
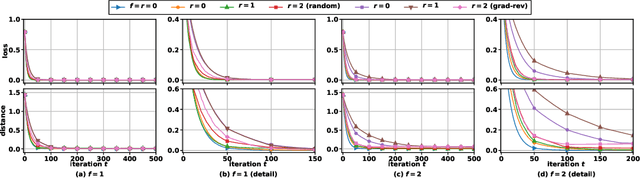
This report considers the problem of Byzantine fault-tolerance in homogeneous multi-agent distributed learning. In this problem, each agent samples i.i.d. data points, and the goal for the agents is to compute a mathematical model that optimally fits, in expectation, the data points sampled by all the agents. We consider the case when a certain number of agents may be Byzantine faulty. Such faulty agents may not follow a prescribed learning algorithm. Faulty agents may share arbitrary incorrect information regarding their data points to prevent the non-faulty agents from learning a correct model. We propose a fault-tolerance mechanism for the distributed stochastic gradient descent (D-SGD) method -- a standard distributed supervised learning algorithm. Our fault-tolerance mechanism relies on a norm based gradient-filter, named comparative gradient elimination (CGE), that aims to mitigate the detrimental impact of malicious incorrect stochastic gradients shared by the faulty agents by limiting their Euclidean norms. We show that the CGE gradient-filter guarantees fault-tolerance against a bounded number of Byzantine faulty agents if the stochastic gradients computed by the non-faulty agents satisfy the standard assumption of bounded variance. We demonstrate the applicability of the CGE gradient-filer for distributed supervised learning of artificial neural networks. We show that the fault-tolerance by the CGE gradient-filter is comparable to that by other state-of-the-art gradient-filters, namely the multi-KRUM, geometric median of means, and coordinate-wise trimmed mean. Lastly, we propose a gradient averaging scheme that aims to reduce the sensitivity of a supervised learning process to individual agents' data batch-sizes. We show that gradient averaging improves the fault-tolerance property of a gradient-filter, including, but not limited to, the CGE gradient-filter.

Randomized Reactive Redundancy for Byzantine Fault-Tolerance in Parallelized Learning

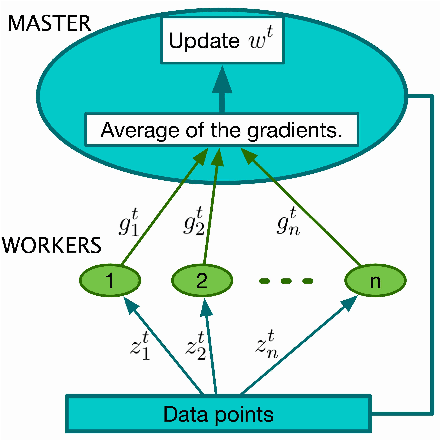
This report considers the problem of Byzantine fault-tolerance in synchronous parallelized learning that is founded on the parallelized stochastic gradient descent (parallelized-SGD) algorithm. The system comprises a master, and $n$ workers, where up to $f$ of the workers are Byzantine faulty. Byzantine workers need not follow the master's instructions correctly, and might send malicious incorrect (or faulty) information. The identity of the Byzantine workers remains fixed throughout the learning process, and is unknown a priori to the master. We propose two coding schemes, a deterministic scheme and a randomized scheme, for guaranteeing exact fault-tolerance if $2f < n$. The coding schemes use the concept of reactive redundancy for isolating Byzantine workers that eventually send faulty information. We note that the computation efficiencies of the schemes compare favorably with other (deterministic or randomized) coding schemes, for exact fault-tolerance.

Byzantine Fault Tolerant Distributed Linear Regression

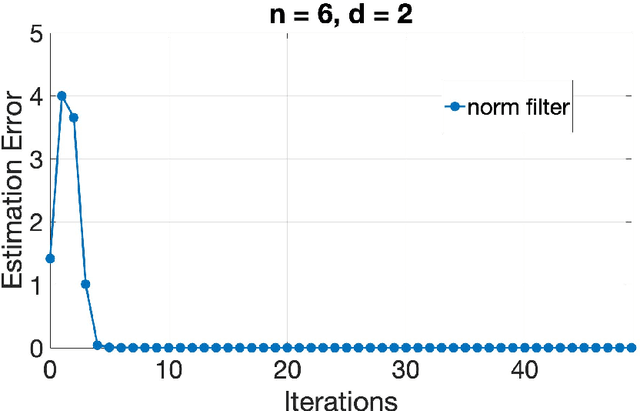
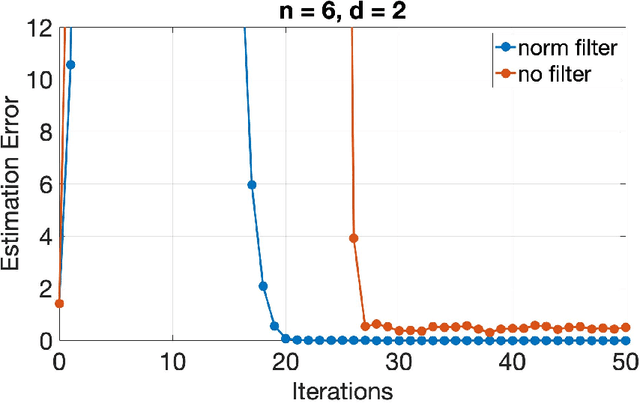
This paper considers the problem of Byzantine fault tolerance in distributed linear regression in a multi-agent system. However, the proposed algorithms are given for a more general class of distributed optimization problems, of which distributed linear regression is a special case. The system comprises of a server and multiple agents, where each agent is holding a certain number of data points and responses that satisfy a linear relationship (could be noisy). The objective of the server is to determine this relationship, given that some of the agents in the system (up to a known number) are Byzantine faulty (aka. actively adversarial). We show that the server can achieve this objective, in a deterministic manner, by robustifying the original distributed gradient descent method using norm based filters, namely 'norm filtering' and 'norm-cap filtering', incurring an additional log-linear computation cost in each iteration. The proposed algorithms improve upon the existing methods on three levels: i) no assumptions are required on the probability distribution of data points, ii) system can be partially asynchronous, and iii) the computational overhead (in order to handle Byzantine faulty agents) is log-linear in number of agents and linear in dimension of data points. The proposed algorithms differ from each other in the assumptions made for their correctness, and the gradient filter they use.

Private Learning on Networks: Part II

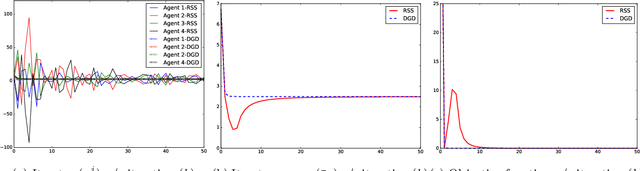
This paper considers a distributed multi-agent optimization problem, with the global objective consisting of the sum of local objective functions of the agents. The agents solve the optimization problem using local computation and communication between adjacent agents in the network. We present two randomized iterative algorithms for distributed optimization. To improve privacy, our algorithms add "structured" randomization to the information exchanged between the agents. We prove deterministic correctness (in every execution) of the proposed algorithms despite the information being perturbed by noise with non-zero mean. We prove that a special case of a proposed algorithm (called function sharing) preserves privacy of individual polynomial objective functions under a suitable connectivity condition on the network topology.

Distributed Optimization for Client-Server Architecture with Negative Gradient Weights

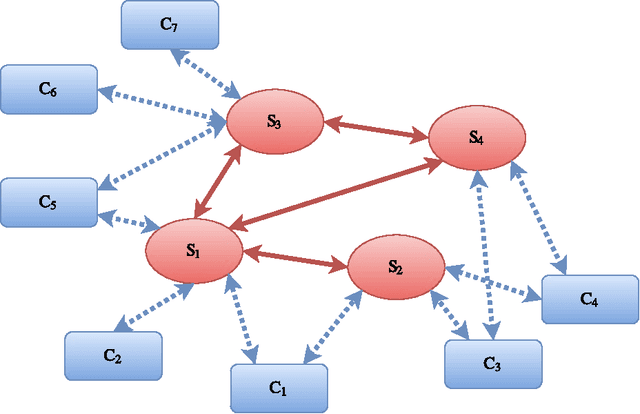
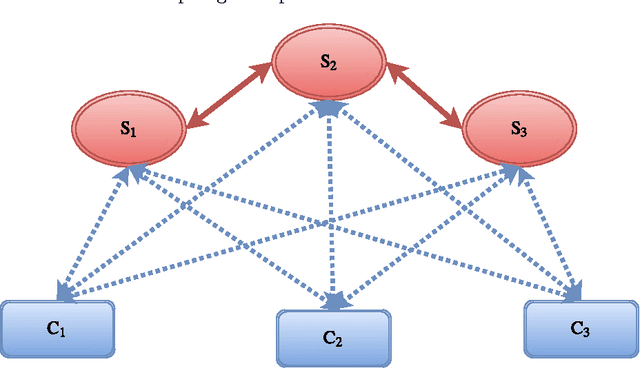
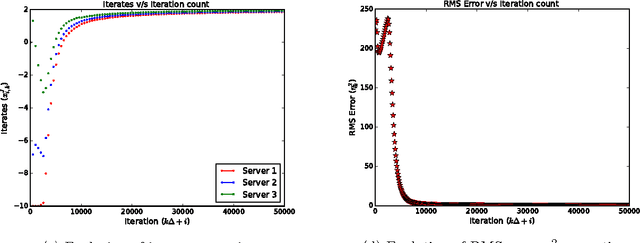
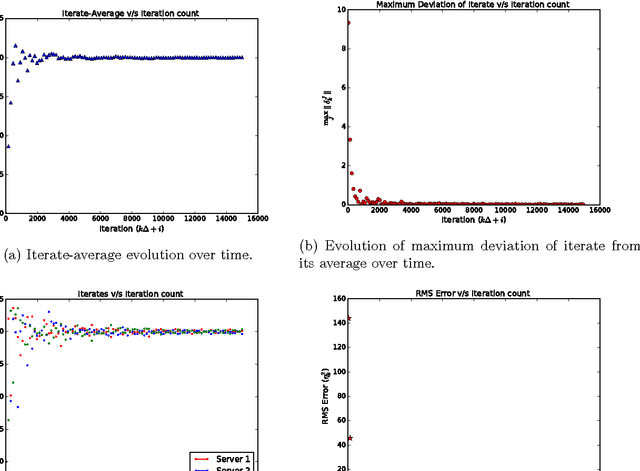
Availability of both massive datasets and computing resources have made machine learning and predictive analytics extremely pervasive. In this work we present a synchronous algorithm and architecture for distributed optimization motivated by privacy requirements posed by applications in machine learning. We present an algorithm for the recently proposed multi-parameter-server architecture. We consider a group of parameter servers that learn a model based on randomized gradients received from clients. Clients are computational entities with private datasets (inducing a private objective function), that evaluate and upload randomized gradients to the parameter servers. The parameter servers perform model updates based on received gradients and share the model parameters with other servers. We prove that the proposed algorithm can optimize the overall objective function for a very general architecture involving $C$ clients connected to $S$ parameter servers in an arbitrary time varying topology and the parameter servers forming a connected network.

Private Learning on Networks

Continual data collection and widespread deployment of machine learning algorithms, particularly the distributed variants, have raised new privacy challenges. In a distributed machine learning scenario, the dataset is stored among several machines and they solve a distributed optimization problem to collectively learn the underlying model. We present a secure multi-party computation inspired privacy preserving distributed algorithm for optimizing a convex function consisting of several possibly non-convex functions. Each individual objective function is privately stored with an agent while the agents communicate model parameters with neighbor machines connected in a network. We show that our algorithm can correctly optimize the overall objective function and learn the underlying model accurately. We further prove that under a vertex connectivity condition on the topology, our algorithm preserves privacy of individual objective functions. We establish limits on the what a coalition of adversaries can learn by observing the messages and states shared over a network.

Distributed Optimization of Convex Sum of Non-Convex Functions

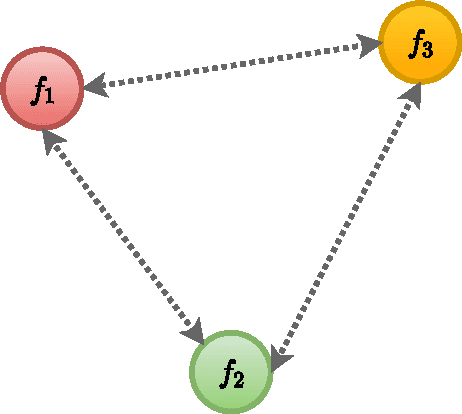
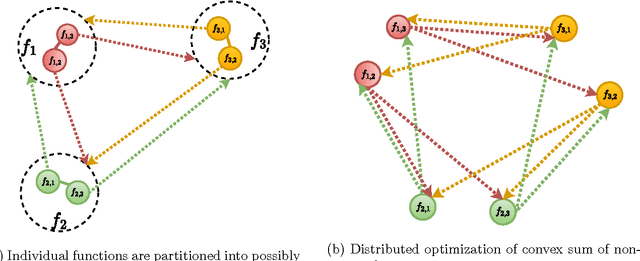
We present a distributed solution to optimizing a convex function composed of several non-convex functions. Each non-convex function is privately stored with an agent while the agents communicate with neighbors to form a network. We show that coupled consensus and projected gradient descent algorithm proposed in [1] can optimize convex sum of non-convex functions under an additional assumption on gradient Lipschitzness. We further discuss the applications of this analysis in improving privacy in distributed optimization.

Defending Non-Bayesian Learning against Adversarial Attacks

This paper addresses the problem of non-Bayesian learning over multi-agent networks, where agents repeatedly collect partially informative observations about an unknown state of the world, and try to collaboratively learn the true state. We focus on the impact of the adversarial agents on the performance of consensus-based non-Bayesian learning, where non-faulty agents combine local learning updates with consensus primitives. In particular, we consider the scenario where an unknown subset of agents suffer Byzantine faults -- agents suffering Byzantine faults behave arbitrarily. Two different learning rules are proposed.