Byzantine Fault-Tolerant Distributed Machine Learning Using Stochastic Gradient Descent (SGD) and Norm-Based Comparative Gradient Elimination (CGE)

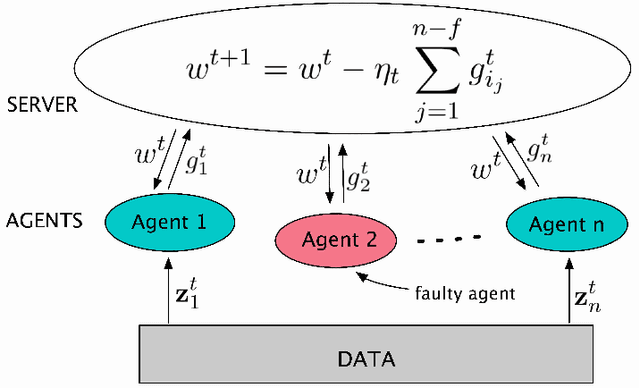
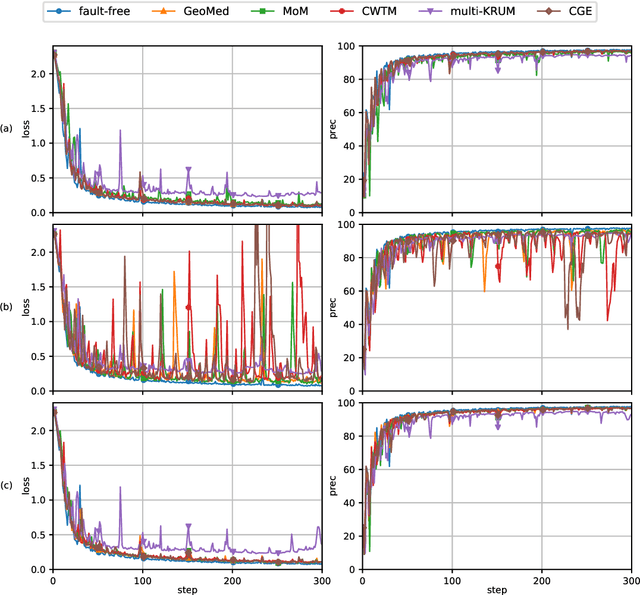
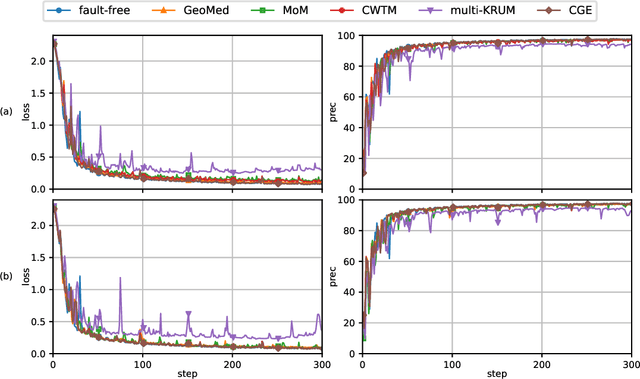
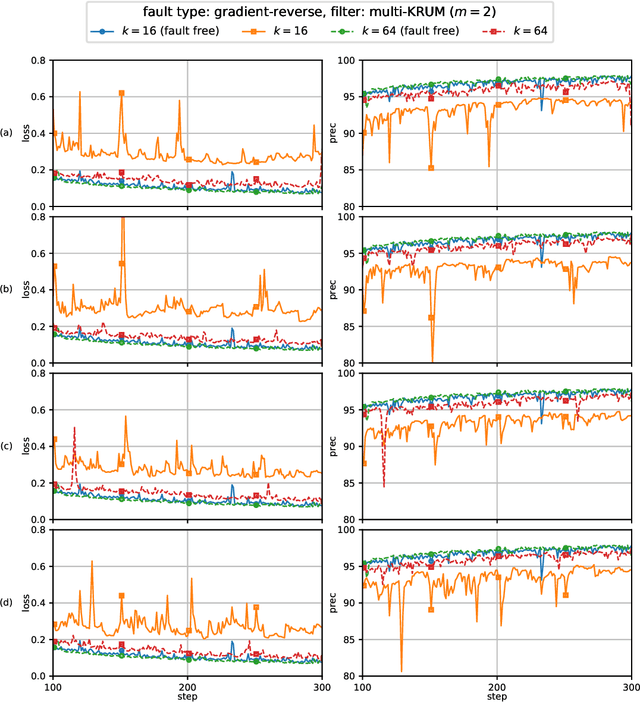
This report considers the problem of Byzantine fault-tolerance in homogeneous multi-agent distributed learning. In this problem, each agent samples i.i.d. data points, and the goal for the agents is to compute a mathematical model that optimally fits, in expectation, the data points sampled by all the agents. We consider the case when a certain number of agents may be Byzantine faulty. Such faulty agents may not follow a prescribed learning algorithm. Faulty agents may share arbitrary incorrect information regarding their data points to prevent the non-faulty agents from learning a correct model. We propose a fault-tolerance mechanism for the distributed stochastic gradient descent (D-SGD) method -- a standard distributed supervised learning algorithm. Our fault-tolerance mechanism relies on a norm based gradient-filter, named comparative gradient elimination (CGE), that aims to mitigate the detrimental impact of malicious incorrect stochastic gradients shared by the faulty agents by limiting their Euclidean norms. We show that the CGE gradient-filter guarantees fault-tolerance against a bounded number of Byzantine faulty agents if the stochastic gradients computed by the non-faulty agents satisfy the standard assumption of bounded variance. We demonstrate the applicability of the CGE gradient-filer for distributed supervised learning of artificial neural networks. We show that the fault-tolerance by the CGE gradient-filter is comparable to that by other state-of-the-art gradient-filters, namely the multi-KRUM, geometric median of means, and coordinate-wise trimmed mean. Lastly, we propose a gradient averaging scheme that aims to reduce the sensitivity of a supervised learning process to individual agents' data batch-sizes. We show that gradient averaging improves the fault-tolerance property of a gradient-filter, including, but not limited to, the CGE gradient-filter.