Distributed Optimization for Client-Server Architecture with Negative Gradient Weights
Paper and Code
Dec 19, 2016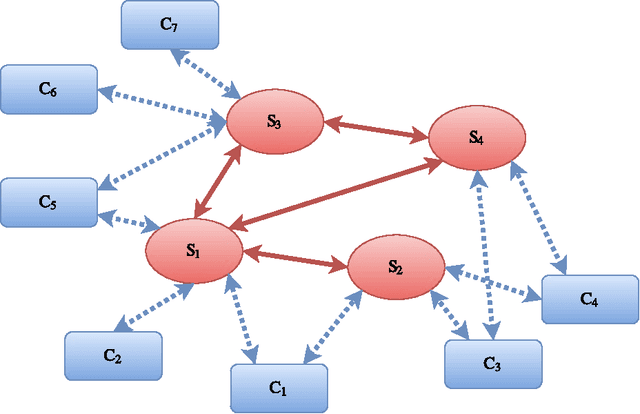
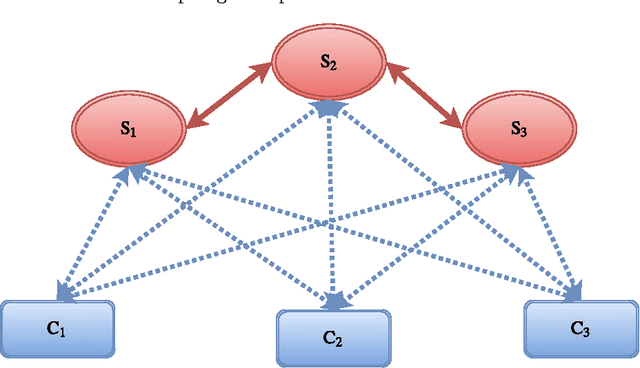
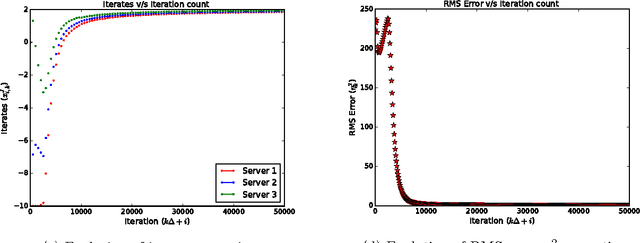
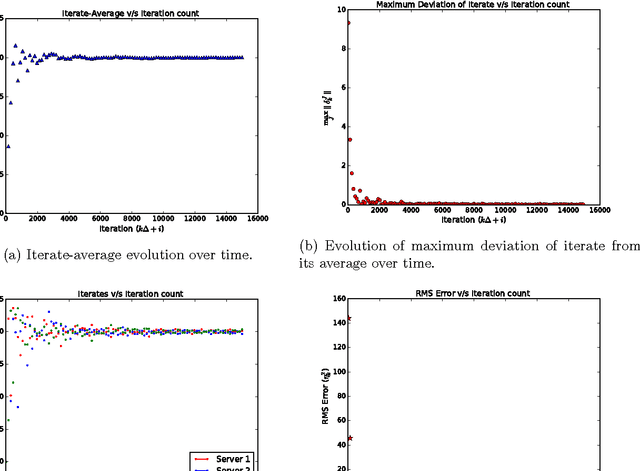
Availability of both massive datasets and computing resources have made machine learning and predictive analytics extremely pervasive. In this work we present a synchronous algorithm and architecture for distributed optimization motivated by privacy requirements posed by applications in machine learning. We present an algorithm for the recently proposed multi-parameter-server architecture. We consider a group of parameter servers that learn a model based on randomized gradients received from clients. Clients are computational entities with private datasets (inducing a private objective function), that evaluate and upload randomized gradients to the parameter servers. The parameter servers perform model updates based on received gradients and share the model parameters with other servers. We prove that the proposed algorithm can optimize the overall objective function for a very general architecture involving $C$ clients connected to $S$ parameter servers in an arbitrary time varying topology and the parameter servers forming a connected network.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge