Byzantine Fault Tolerant Distributed Linear Regression
Paper and Code
Apr 04, 2019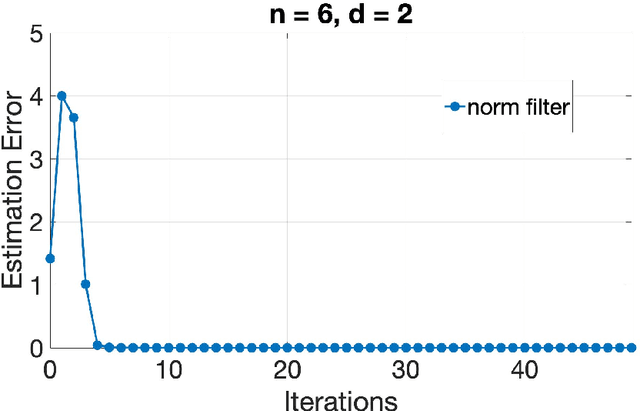
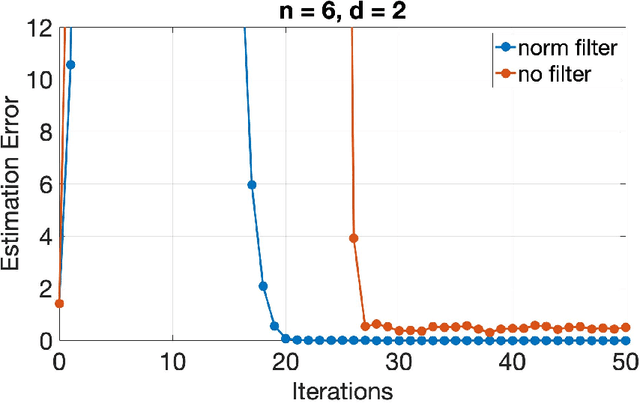
This paper considers the problem of Byzantine fault tolerance in distributed linear regression in a multi-agent system. However, the proposed algorithms are given for a more general class of distributed optimization problems, of which distributed linear regression is a special case. The system comprises of a server and multiple agents, where each agent is holding a certain number of data points and responses that satisfy a linear relationship (could be noisy). The objective of the server is to determine this relationship, given that some of the agents in the system (up to a known number) are Byzantine faulty (aka. actively adversarial). We show that the server can achieve this objective, in a deterministic manner, by robustifying the original distributed gradient descent method using norm based filters, namely 'norm filtering' and 'norm-cap filtering', incurring an additional log-linear computation cost in each iteration. The proposed algorithms improve upon the existing methods on three levels: i) no assumptions are required on the probability distribution of data points, ii) system can be partially asynchronous, and iii) the computational overhead (in order to handle Byzantine faulty agents) is log-linear in number of agents and linear in dimension of data points. The proposed algorithms differ from each other in the assumptions made for their correctness, and the gradient filter they use.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge