Distributed Optimization of Convex Sum of Non-Convex Functions

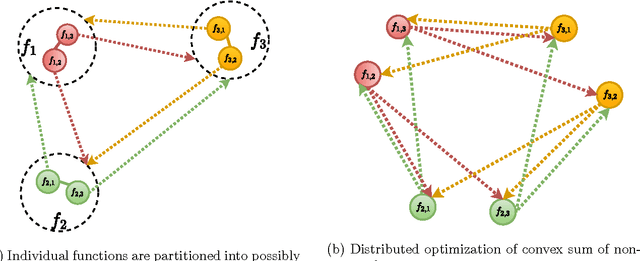
We present a distributed solution to optimizing a convex function composed of several non-convex functions. Each non-convex function is privately stored with an agent while the agents communicate with neighbors to form a network. We show that coupled consensus and projected gradient descent algorithm proposed in [1] can optimize convex sum of non-convex functions under an additional assumption on gradient Lipschitzness. We further discuss the applications of this analysis in improving privacy in distributed optimization.