Experimentation Accelerator: Interpretable Insights and Creative Recommendations for A/B Testing with Content-Aware ranking

Modern online experimentation faces two bottlenecks: scarce traffic forces tough choices on which variants to test, and post-hoc insight extraction is manual, inconsistent, and often content-agnostic. Meanwhile, organizations underuse historical A/B results and rich content embeddings that could guide prioritization and creative iteration. We present a unified framework to (i) prioritize which variants to test, (ii) explain why winners win, and (iii) surface targeted opportunities for new, higher-potential variants. Leveraging treatment embeddings and historical outcomes, we train a CTR ranking model with fixed effects for contextual shifts that scores candidates while balancing value and content diversity. For better interpretability and understanding, we project treatments onto curated semantic marketing attributes and re-express the ranker in this space via a sign-consistent, sparse constrained Lasso, yielding per-attribute coefficients and signed contributions for visual explanations, top-k drivers, and natural-language insights. We then compute an opportunity index combining attribute importance (from the ranker) with under-expression in the current experiment to flag missing, high-impact attributes. Finally, LLMs translate ranked opportunities into concrete creative suggestions and estimate both learning and conversion potential, enabling faster, more informative, and more efficient test cycles. These components have been built into a real Adobe product, called \textit{Experimentation Accelerator}, to provide AI-based insights and opportunities to scale experimentation for customers. We provide an evaluation of the performance of the proposed framework on some real-world experiments by Adobe business customers that validate the high quality of the generation pipeline.

Relational Causal Discovery with Latent Confounders

Estimating causal effects from real-world relational data can be challenging when the underlying causal model and potential confounders are unknown. While several causal discovery algorithms exist for learning causal models with latent confounders from data, they assume that the data is independent and identically distributed (i.i.d.) and are not well-suited for learning from relational data. Similarly, existing relational causal discovery algorithms assume causal sufficiency, which is unrealistic for many real-world datasets. To address this gap, we propose RelFCI, a sound and complete causal discovery algorithm for relational data with latent confounders. Our work builds upon the Fast Causal Inference (FCI) and Relational Causal Discovery (RCD) algorithms and it defines new graphical models, necessary to support causal discovery in relational domains. We also establish soundness and completeness guarantees for relational d-separation with latent confounders. We present experimental results demonstrating the effectiveness of RelFCI in identifying the correct causal structure in relational causal models with latent confounders.

Principled Content Selection to Generate Diverse and Personalized Multi-Document Summaries

While large language models (LLMs) are increasingly capable of handling longer contexts, recent work has demonstrated that they exhibit the "lost in the middle" phenomenon (Liu et al., 2024) of unevenly attending to different parts of the provided context. This hinders their ability to cover diverse source material in multi-document summarization, as noted in the DiverseSumm benchmark (Huang et al., 2024). In this work, we contend that principled content selection is a simple way to increase source coverage on this task. As opposed to prompting an LLM to perform the summarization in a single step, we explicitly divide the task into three steps -- (1) reducing document collections to atomic key points, (2) using determinantal point processes (DPP) to perform select key points that prioritize diverse content, and (3) rewriting to the final summary. By combining prompting steps, for extraction and rewriting, with principled techniques, for content selection, we consistently improve source coverage on the DiverseSumm benchmark across various LLMs. Finally, we also show that by incorporating relevance to a provided user intent into the DPP kernel, we can generate personalized summaries that cover relevant source information while retaining coverage.

Evaluation and Incident Prevention in an Enterprise AI Assistant

Enterprise AI Assistants are increasingly deployed in domains where accuracy is paramount, making each erroneous output a potentially significant incident. This paper presents a comprehensive framework for monitoring, benchmarking, and continuously improving such complex, multi-component systems under active development by multiple teams. Our approach encompasses three key elements: (1) a hierarchical ``severity'' framework for incident detection that identifies and categorizes errors while attributing component-specific error rates, facilitating targeted improvements; (2) a scalable and principled methodology for benchmark construction, evaluation, and deployment, designed to accommodate multiple development teams, mitigate overfitting risks, and assess the downstream impact of system modifications; and (3) a continual improvement strategy leveraging multidimensional evaluation, enabling the identification and implementation of diverse enhancement opportunities. By adopting this holistic framework, organizations can systematically enhance the reliability and performance of their AI Assistants, ensuring their efficacy in critical enterprise environments. We conclude by discussing how this multifaceted evaluation approach opens avenues for various classes of enhancements, paving the way for more robust and trustworthy AI systems.

Continuous Treatment Effects with Surrogate Outcomes

In many real-world causal inference applications, the primary outcomes (labels) are often partially missing, especially if they are expensive or difficult to collect. If the missingness depends on covariates (i.e., missingness is not completely at random), analyses based on fully-observed samples alone may be biased. Incorporating surrogates, which are fully observed post-treatment variables related to the primary outcome, can improve estimation in this case. In this paper, we study the role of surrogates in estimating continuous treatment effects and propose a doubly robust method to efficiently incorporate surrogates in the analysis, which uses both labeled and unlabeled data and does not suffer from the above selection bias problem. Importantly, we establish asymptotic normality of the proposed estimator and show possible improvements on the variance compared with methods that solely use labeled data. Extensive simulations show our methods enjoy appealing empirical performance.

Leveraging Graph Diffusion Models for Network Refinement Tasks

Most real-world networks are noisy and incomplete samples from an unknown target distribution. Refining them by correcting corruptions or inferring unobserved regions typically improves downstream performance. Inspired by the impressive generative capabilities that have been used to correct corruptions in images, and the similarities between "in-painting" and filling in missing nodes and edges conditioned on the observed graph, we propose a novel graph generative framework, SGDM, which is based on subgraph diffusion. Our framework not only improves the scalability and fidelity of graph diffusion models, but also leverages the reverse process to perform novel, conditional generation tasks. In particular, through extensive empirical analysis and a set of novel metrics, we demonstrate that our proposed model effectively supports the following refinement tasks for partially observable networks: T1: denoising extraneous subgraphs, T2: expanding existing subgraphs and T3: performing "style" transfer by regenerating a particular subgraph to match the characteristics of a different node or subgraph.

Distributional Off-Policy Evaluation for Slate Recommendations

Recommendation strategies are typically evaluated by using previously logged data, employing off-policy evaluation methods to estimate their expected performance. However, for strategies that present users with slates of multiple items, the resulting combinatorial action space renders many of these methods impractical. Prior work has developed estimators that leverage the structure in slates to estimate the expected off-policy performance, but the estimation of the entire performance distribution remains elusive. Estimating the complete distribution allows for a more comprehensive evaluation of recommendation strategies, particularly along the axes of risk and fairness that employ metrics computable from the distribution. In this paper, we propose an estimator for the complete off-policy performance distribution for slates and establish conditions under which the estimator is unbiased and consistent. This builds upon prior work on off-policy evaluation for slates and off-policy distribution estimation in reinforcement learning. We validate the efficacy of our method empirically on synthetic data as well as on a slate recommendation simulator constructed from real-world data (MovieLens-20M). Our results show a significant reduction in estimation variance and improved sample efficiency over prior work across a range of slate structures.

Sample Constrained Treatment Effect Estimation

Treatment effect estimation is a fundamental problem in causal inference. We focus on designing efficient randomized controlled trials, to accurately estimate the effect of some treatment on a population of $n$ individuals. In particular, we study sample-constrained treatment effect estimation, where we must select a subset of $s \ll n$ individuals from the population to experiment on. This subset must be further partitioned into treatment and control groups. Algorithms for partitioning the entire population into treatment and control groups, or for choosing a single representative subset, have been well-studied. The key challenge in our setting is jointly choosing a representative subset and a partition for that set. We focus on both individual and average treatment effect estimation, under a linear effects model. We give provably efficient experimental designs and corresponding estimators, by identifying connections to discrepancy minimization and leverage-score-based sampling used in randomized numerical linear algebra. Our theoretical results obtain a smooth transition to known guarantees when $s$ equals the population size. We also empirically demonstrate the performance of our algorithms.

Learning Relational Causal Models with Cycles through Relational Acyclification

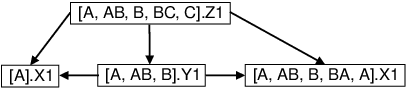
In real-world phenomena which involve mutual influence or causal effects between interconnected units, equilibrium states are typically represented with cycles in graphical models. An expressive class of graphical models, \textit{relational causal models}, can represent and reason about complex dynamic systems exhibiting such cycles or feedback loops. Existing cyclic causal discovery algorithms for learning causal models from observational data assume that the data instances are independent and identically distributed which makes them unsuitable for relational causal models. At the same time, causal discovery algorithms for relational causal models assume acyclicity. In this work, we examine the necessary and sufficient conditions under which a constraint-based relational causal discovery algorithm is sound and complete for \textit{cyclic relational causal models}. We introduce \textit{relational acyclification}, an operation specifically designed for relational models that enables reasoning about the identifiability of cyclic relational causal models. We show that under the assumptions of relational acyclification and $\sigma$-faithfulness, the relational causal discovery algorithm RCD (Maier et al. 2013) is sound and complete for cyclic models. We present experimental results to support our claim.

Non-Parametric Inference of Relational Dependence

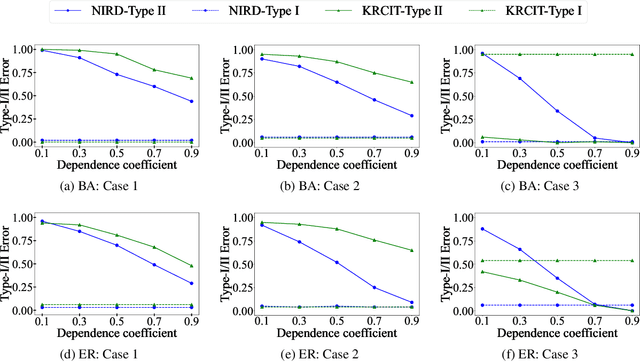
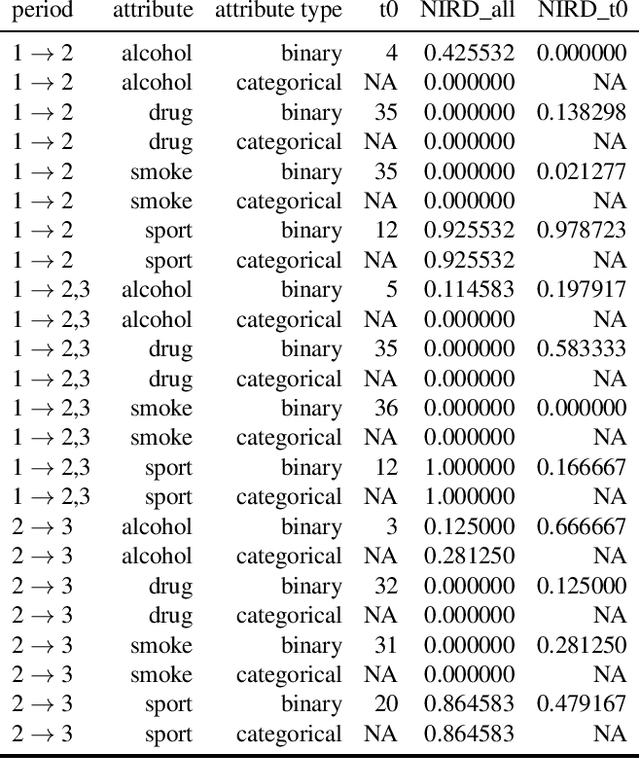
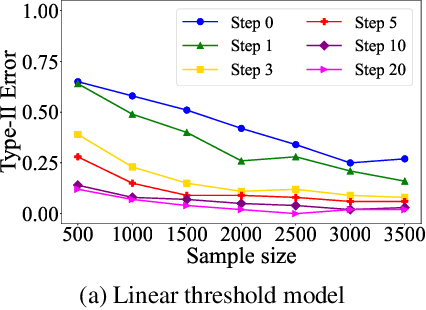
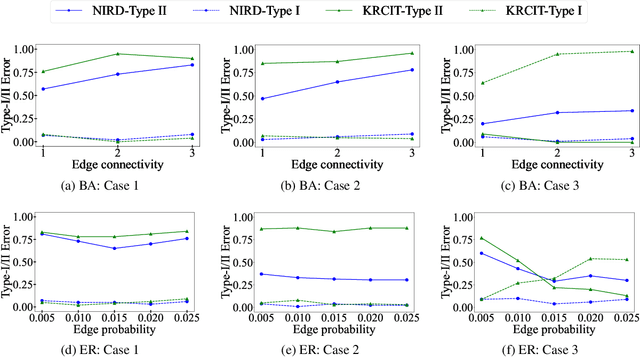
Independence testing plays a central role in statistical and causal inference from observational data. Standard independence tests assume that the data samples are independent and identically distributed (i.i.d.) but that assumption is violated in many real-world datasets and applications centered on relational systems. This work examines the problem of estimating independence in data drawn from relational systems by defining sufficient representations for the sets of observations influencing individual instances. Specifically, we define marginal and conditional independence tests for relational data by considering the kernel mean embedding as a flexible aggregation function for relational variables. We propose a consistent, non-parametric, scalable kernel test to operationalize the relational independence test for non-i.i.d. observational data under a set of structural assumptions. We empirically evaluate our proposed method on a variety of synthetic and semi-synthetic networks and demonstrate its effectiveness compared to state-of-the-art kernel-based independence tests.