Large Generative Graph Models

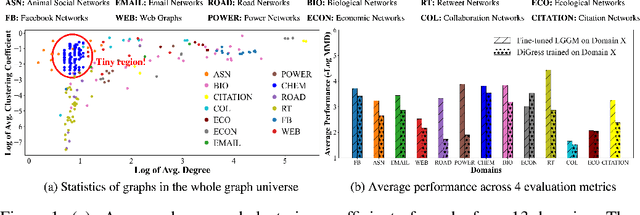
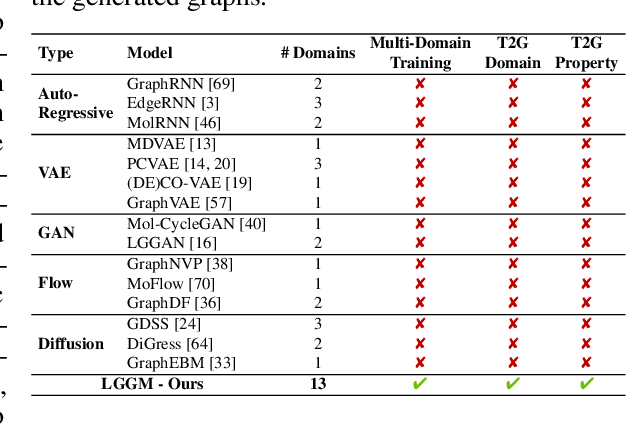
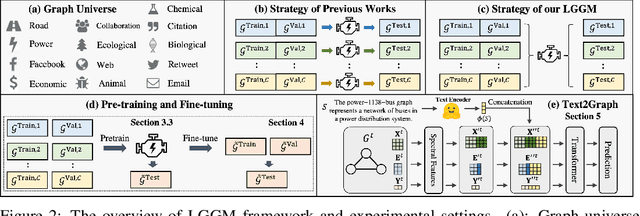
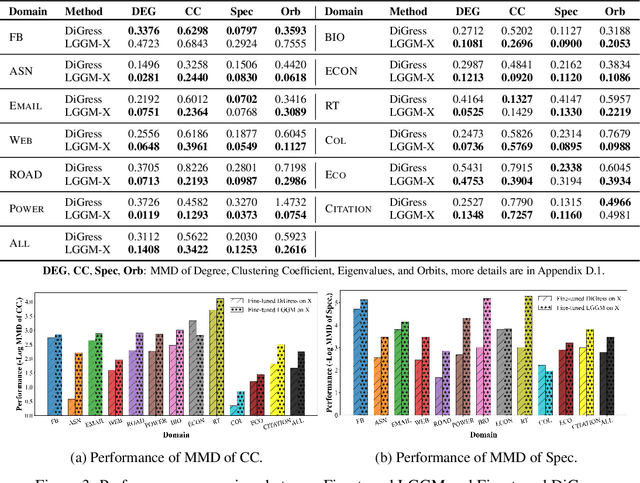
Large Generative Models (LGMs) such as GPT, Stable Diffusion, Sora, and Suno are trained on a huge amount of language corpus, images, videos, and audio that are extremely diverse from numerous domains. This training paradigm over diverse well-curated data lies at the heart of generating creative and sensible content. However, all previous graph generative models (e.g., GraphRNN, MDVAE, MoFlow, GDSS, and DiGress) have been trained only on one dataset each time, which cannot replicate the revolutionary success achieved by LGMs in other fields. To remedy this crucial gap, we propose a new class of graph generative model called Large Graph Generative Model (LGGM) that is trained on a large corpus of graphs (over 5000 graphs) from 13 different domains. We empirically demonstrate that the pre-trained LGGM has superior zero-shot generative capability to existing graph generative models. Furthermore, our pre-trained LGGM can be easily fine-tuned with graphs from target domains and demonstrate even better performance than those directly trained from scratch, behaving as a solid starting point for real-world customization. Inspired by Stable Diffusion, we further equip LGGM with the capability to generate graphs given text prompts (Text-to-Graph), such as the description of the network name and domain (i.e., "The power-1138-bus graph represents a network of buses in a power distribution system."), and network statistics (i.e., "The graph has a low average degree, suitable for modeling social media interactions."). This Text-to-Graph capability integrates the extensive world knowledge in the underlying language model, offering users fine-grained control of the generated graphs. We release the code, the model checkpoint, and the datasets at https://lggm-lg.github.io/.

Forward Learning of Graph Neural Networks

Graph neural networks (GNNs) have achieved remarkable success across a wide range of applications, such as recommendation, drug discovery, and question answering. Behind the success of GNNs lies the backpropagation (BP) algorithm, which is the de facto standard for training deep neural networks (NNs). However, despite its effectiveness, BP imposes several constraints, which are not only biologically implausible, but also limit the scalability, parallelism, and flexibility in learning NNs. Examples of such constraints include storage of neural activities computed in the forward pass for use in the subsequent backward pass, and the dependence of parameter updates on non-local signals. To address these limitations, the forward-forward algorithm (FF) was recently proposed as an alternative to BP in the image classification domain, which trains NNs by performing two forward passes over positive and negative data. Inspired by this advance, we propose ForwardGNN in this work, a new forward learning procedure for GNNs, which avoids the constraints imposed by BP via an effective layer-wise local forward training. ForwardGNN extends the original FF to deal with graph data and GNNs, and makes it possible to operate without generating negative inputs (hence no longer forward-forward). Further, ForwardGNN enables each layer to learn from both the bottom-up and top-down signals without relying on the backpropagation of errors. Extensive experiments on real-world datasets show the effectiveness and generality of the proposed forward graph learning framework. We release our code at https://github.com/facebookresearch/forwardgnn.

Accurate and Scalable Estimation of Epistemic Uncertainty for Graph Neural Networks

While graph neural networks (GNNs) are widely used for node and graph representation learning tasks, the reliability of GNN uncertainty estimates under distribution shifts remains relatively under-explored. Indeed, while post-hoc calibration strategies can be used to improve in-distribution calibration, they need not also improve calibration under distribution shift. However, techniques which produce GNNs with better intrinsic uncertainty estimates are particularly valuable, as they can always be combined with post-hoc strategies later. Therefore, in this work, we propose G-$\Delta$UQ, a novel training framework designed to improve intrinsic GNN uncertainty estimates. Our framework adapts the principle of stochastic data centering to graph data through novel graph anchoring strategies, and is able to support partially stochastic GNNs. While, the prevalent wisdom is that fully stochastic networks are necessary to obtain reliable estimates, we find that the functional diversity induced by our anchoring strategies when sampling hypotheses renders this unnecessary and allows us to support G-$\Delta$UQ on pretrained models. Indeed, through extensive evaluation under covariate, concept and graph size shifts, we show that G-$\Delta$UQ leads to better calibrated GNNs for node and graph classification. Further, it also improves performance on the uncertainty-based tasks of out-of-distribution detection and generalization gap estimation. Overall, our work provides insights into uncertainty estimation for GNNs, and demonstrates the utility of G-$\Delta$UQ in obtaining reliable estimates.

Leveraging Graph Diffusion Models for Network Refinement Tasks

Most real-world networks are noisy and incomplete samples from an unknown target distribution. Refining them by correcting corruptions or inferring unobserved regions typically improves downstream performance. Inspired by the impressive generative capabilities that have been used to correct corruptions in images, and the similarities between "in-painting" and filling in missing nodes and edges conditioned on the observed graph, we propose a novel graph generative framework, SGDM, which is based on subgraph diffusion. Our framework not only improves the scalability and fidelity of graph diffusion models, but also leverages the reverse process to perform novel, conditional generation tasks. In particular, through extensive empirical analysis and a set of novel metrics, we demonstrate that our proposed model effectively supports the following refinement tasks for partially observable networks: T1: denoising extraneous subgraphs, T2: expanding existing subgraphs and T3: performing "style" transfer by regenerating a particular subgraph to match the characteristics of a different node or subgraph.

PAGER: A Framework for Failure Analysis of Deep Regression Models

Safe deployment of AI models requires proactive detection of potential prediction failures to prevent costly errors. While failure detection in classification problems has received significant attention, characterizing failure modes in regression tasks is more complicated and less explored. Existing approaches rely on epistemic uncertainties or feature inconsistency with the training distribution to characterize model risk. However, we show that uncertainties are necessary but insufficient to accurately characterize failure, owing to the various sources of error. In this paper, we propose PAGER (Principled Analysis of Generalization Errors in Regressors), a framework to systematically detect and characterize failures in deep regression models. Built upon the recently proposed idea of anchoring in deep models, PAGER unifies both epistemic uncertainties and novel, complementary non-conformity scores to organize samples into different risk regimes, thereby providing a comprehensive analysis of model errors. Additionally, we introduce novel metrics for evaluating failure detectors in regression tasks. We demonstrate the effectiveness of PAGER on synthetic and real-world benchmarks. Our results highlight the capability of PAGER to identify regions of accurate generalization and detect failure cases in out-of-distribution and out-of-support scenarios.

Fairness-Aware Graph Neural Networks: A Survey

Graph Neural Networks (GNNs) have become increasingly important due to their representational power and state-of-the-art predictive performance on many fundamental learning tasks. Despite this success, GNNs suffer from fairness issues that arise as a result of the underlying graph data and the fundamental aggregation mechanism that lies at the heart of the large class of GNN models. In this article, we examine and categorize fairness techniques for improving the fairness of GNNs. Previous work on fair GNN models and techniques are discussed in terms of whether they focus on improving fairness during a preprocessing step, during training, or in a post-processing phase. Furthermore, we discuss how such techniques can be used together whenever appropriate, and highlight the advantages and intuition as well. We also introduce an intuitive taxonomy for fairness evaluation metrics including graph-level fairness, neighborhood-level fairness, embedding-level fairness, and prediction-level fairness metrics. In addition, graph datasets that are useful for benchmarking the fairness of GNN models are summarized succinctly. Finally, we highlight key open problems and challenges that remain to be addressed.

A Closer Look at Model Adaptation using Feature Distortion and Simplicity Bias

Advances in the expressivity of pretrained models have increased interest in the design of adaptation protocols which enable safe and effective transfer learning. Going beyond conventional linear probing (LP) and fine tuning (FT) strategies, protocols that can effectively control feature distortion, i.e., the failure to update features orthogonal to the in-distribution, have been found to achieve improved out-of-distribution generalization (OOD). In order to limit this distortion, the LP+FT protocol, which first learns a linear probe and then uses this initialization for subsequent FT, was proposed. However, in this paper, we find when adaptation protocols (LP, FT, LP+FT) are also evaluated on a variety of safety objectives (e.g., calibration, robustness, etc.), a complementary perspective to feature distortion is helpful to explain protocol behavior. To this end, we study the susceptibility of protocols to simplicity bias (SB), i.e. the well-known propensity of deep neural networks to rely upon simple features, as SB has recently been shown to underlie several problems in robust generalization. Using a synthetic dataset, we demonstrate the susceptibility of existing protocols to SB. Given the strong effectiveness of LP+FT, we then propose modified linear probes that help mitigate SB, and lead to better initializations for subsequent FT. We verify the effectiveness of the proposed LP+FT variants for decreasing SB in a controlled setting, and their ability to improve OOD generalization and safety on three adaptation datasets.

A Closer Look at Scoring Functions and Generalization Prediction

Generalization error predictors (GEPs) aim to predict model performance on unseen distributions by deriving dataset-level error estimates from sample-level scores. However, GEPs often utilize disparate mechanisms (e.g., regressors, thresholding functions, calibration datasets, etc), to derive such error estimates, which can obfuscate the benefits of a particular scoring function. Therefore, in this work, we rigorously study the effectiveness of popular scoring functions (confidence, local manifold smoothness, model agreement), independent of mechanism choice. We find, absent complex mechanisms, that state-of-the-art confidence- and smoothness- based scores fail to outperform simple model-agreement scores when estimating error under distribution shifts and corruptions. Furthermore, on realistic settings where the training data has been compromised (e.g., label noise, measurement noise, undersampling), we find that model-agreement scores continue to perform well and that ensemble diversity is important for improving its performance. Finally, to better understand the limitations of scoring functions, we demonstrate that simplicity bias, or the propensity of deep neural networks to rely upon simple but brittle features, can adversely affect GEP performance. Overall, our work carefully studies the effectiveness of popular scoring functions in realistic settings and helps to better understand their limitations.

Analyzing Data-Centric Properties for Contrastive Learning on Graphs

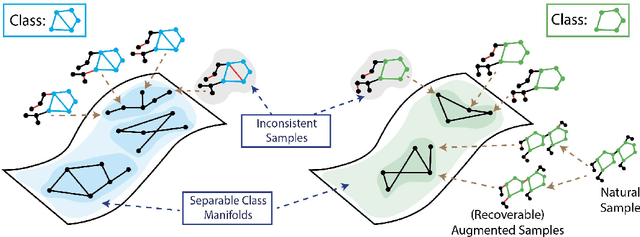
Recent analyses of self-supervised learning (SSL) find the following data-centric properties to be critical for learning good representations: invariance to task-irrelevant semantics, separability of classes in some latent space, and recoverability of labels from augmented samples. However, given their discrete, non-Euclidean nature, graph datasets and graph SSL methods are unlikely to satisfy these properties. This raises the question: how do graph SSL methods, such as contrastive learning (CL), work well? To systematically probe this question, we perform a generalization analysis for CL when using generic graph augmentations (GGAs), with a focus on data-centric properties. Our analysis yields formal insights into the limitations of GGAs and the necessity of task-relevant augmentations. As we empirically show, GGAs do not induce task-relevant invariances on common benchmark datasets, leading to only marginal gains over naive, untrained baselines. Our theory motivates a synthetic data generation process that enables control over task-relevant information and boasts pre-defined optimal augmentations. This flexible benchmark helps us identify yet unrecognized limitations in advanced augmentation techniques (e.g., automated methods). Overall, our work rigorously contextualizes, both empirically and theoretically, the effects of data-centric properties on augmentation strategies and learning paradigms for graph SSL.

Exploring the Design of Adaptation Protocols for Improved Generalization and Machine Learning Safety

While directly fine-tuning (FT) large-scale, pretrained models on task-specific data is well-known to induce strong in-distribution task performance, recent works have demonstrated that different adaptation protocols, such as linear probing (LP) prior to FT, can improve out-of-distribution generalization. However, the design space of such adaptation protocols remains under-explored and the evaluation of such protocols has primarily focused on distribution shifts. Therefore, in this work, we evaluate common adaptation protocols across distributions shifts and machine learning safety metrics (e.g., anomaly detection, calibration, robustness to corruptions). We find that protocols induce disparate trade-offs that were not apparent from prior evaluation. Further, we demonstrate that appropriate pairing of data augmentation and protocol can substantially mitigate this trade-off. Finally, we hypothesize and empirically see that using hardness-promoting augmentations during LP and then FT with augmentations may be particularly effective for trade-off mitigation.