Accurate and Scalable Estimation of Epistemic Uncertainty for Graph Neural Networks

While graph neural networks (GNNs) are widely used for node and graph representation learning tasks, the reliability of GNN uncertainty estimates under distribution shifts remains relatively under-explored. Indeed, while post-hoc calibration strategies can be used to improve in-distribution calibration, they need not also improve calibration under distribution shift. However, techniques which produce GNNs with better intrinsic uncertainty estimates are particularly valuable, as they can always be combined with post-hoc strategies later. Therefore, in this work, we propose G-$\Delta$UQ, a novel training framework designed to improve intrinsic GNN uncertainty estimates. Our framework adapts the principle of stochastic data centering to graph data through novel graph anchoring strategies, and is able to support partially stochastic GNNs. While, the prevalent wisdom is that fully stochastic networks are necessary to obtain reliable estimates, we find that the functional diversity induced by our anchoring strategies when sampling hypotheses renders this unnecessary and allows us to support G-$\Delta$UQ on pretrained models. Indeed, through extensive evaluation under covariate, concept and graph size shifts, we show that G-$\Delta$UQ leads to better calibrated GNNs for node and graph classification. Further, it also improves performance on the uncertainty-based tasks of out-of-distribution detection and generalization gap estimation. Overall, our work provides insights into uncertainty estimation for GNNs, and demonstrates the utility of G-$\Delta$UQ in obtaining reliable estimates.

On Performance Discrepancies Across Local Homophily Levels in Graph Neural Networks

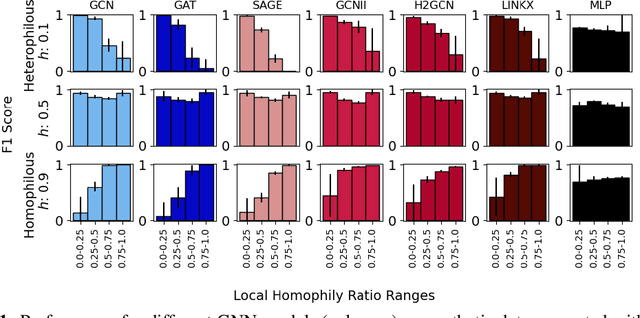
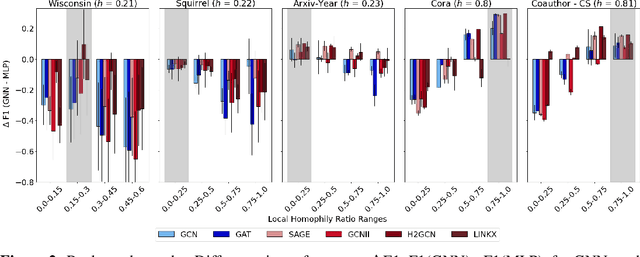
Research on GNNs has highlighted a relationship between high homophily (i.e., the tendency for nodes of a similar class to connect) and strong predictive performance in node classification. However, recent research has found the relationship to be more nuanced, demonstrating that even simple GNNs can learn in certain heterophilous settings. To bridge the gap between these findings, we revisit the assumptions made in previous works and identify that datasets are often treated as having a constant homophily level across nodes. To align closer to real-world datasets, we theoretically and empirically study the performance of GNNs when the local homophily level of a node deviates at test-time from the global homophily level of its graph. To aid our theoretical analysis, we introduce a new parameter to the preferential attachment model commonly used in homophily analysis to enable the control of local homophily levels in generated graphs, enabling a systematic empirical study on how local homophily can impact performance. We additionally perform a granular analysis on a number of real-world datasets with varying global homophily levels. Across our theoretical and empirical results, we find that (a)~ GNNs can fail to generalize to test nodes that deviate from the global homophily of a graph, (b)~ high local homophily does not necessarily confer high performance for a node, and (c)~ GNN models designed to handle heterophily are able to perform better across varying heterophily ranges irrespective of the dataset's global homophily. These findings point towards a GNN's over-reliance on the global homophily used for training and motivates the need to design GNNs that can better generalize across large local homophily ranges.

CAPER: Coarsen, Align, Project, Refine - A General Multilevel Framework for Network Alignment

Network alignment, or the task of finding corresponding nodes in different networks, is an important problem formulation in many application domains. We propose CAPER, a multilevel alignment framework that Coarsens the input graphs, Aligns the coarsened graphs, Projects the alignment solution to finer levels and Refines the alignment solution. We show that CAPER can improve upon many different existing network alignment algorithms by enforcing alignment consistency across multiple graph resolutions: nodes matched at finer levels should also be matched at coarser levels. CAPER also accelerates the use of slower network alignment methods, at the modest cost of linear-time coarsening and refinement steps, by allowing them to be run on smaller coarsened versions of the input graphs. Experiments show that CAPER can improve upon diverse network alignment methods by an average of 33% in accuracy and/or an order of magnitude faster in runtime.

Analyzing Data-Centric Properties for Contrastive Learning on Graphs

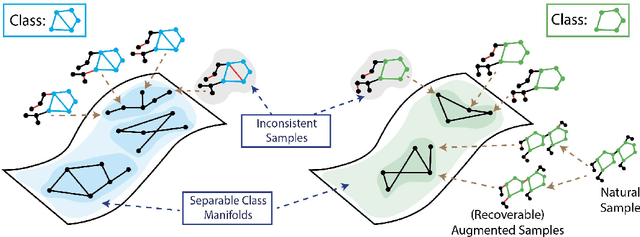
Recent analyses of self-supervised learning (SSL) find the following data-centric properties to be critical for learning good representations: invariance to task-irrelevant semantics, separability of classes in some latent space, and recoverability of labels from augmented samples. However, given their discrete, non-Euclidean nature, graph datasets and graph SSL methods are unlikely to satisfy these properties. This raises the question: how do graph SSL methods, such as contrastive learning (CL), work well? To systematically probe this question, we perform a generalization analysis for CL when using generic graph augmentations (GGAs), with a focus on data-centric properties. Our analysis yields formal insights into the limitations of GGAs and the necessity of task-relevant augmentations. As we empirically show, GGAs do not induce task-relevant invariances on common benchmark datasets, leading to only marginal gains over naive, untrained baselines. Our theory motivates a synthetic data generation process that enables control over task-relevant information and boasts pre-defined optimal augmentations. This flexible benchmark helps us identify yet unrecognized limitations in advanced augmentation techniques (e.g., automated methods). Overall, our work rigorously contextualizes, both empirically and theoretically, the effects of data-centric properties on augmentation strategies and learning paradigms for graph SSL.

Contrastive Knowledge-Augmented Meta-Learning for Few-Shot Classification

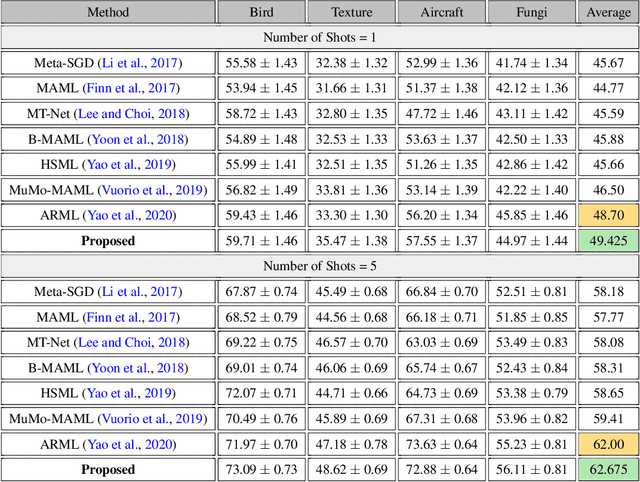
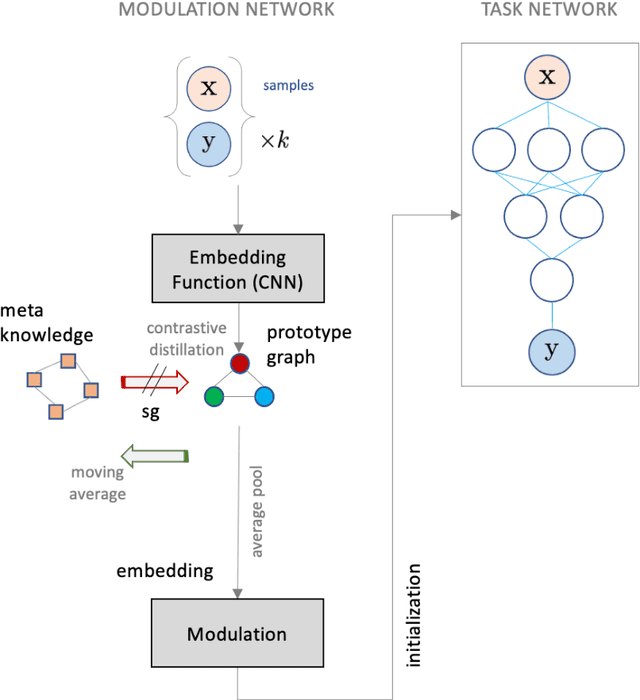
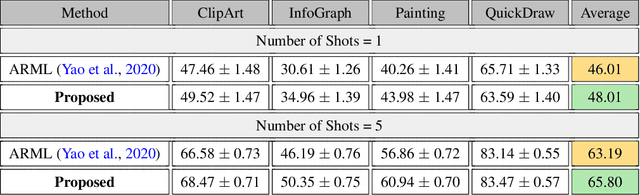
Model agnostic meta-learning algorithms aim to infer priors from several observed tasks that can then be used to adapt to a new task with few examples. Given the inherent diversity of tasks arising in existing benchmarks, recent methods use separate, learnable structure, such as hierarchies or graphs, for enabling task-specific adaptation of the prior. While these approaches have produced significantly better meta learners, our goal is to improve their performance when the heterogeneous task distribution contains challenging distribution shifts and semantic disparities. To this end, we introduce CAML (Contrastive Knowledge-Augmented Meta Learning), a novel approach for knowledge-enhanced few-shot learning that evolves a knowledge graph to effectively encode historical experience, and employs a contrastive distillation strategy to leverage the encoded knowledge for task-aware modulation of the base learner. Using standard benchmarks, we evaluate the performance of CAML in different few-shot learning scenarios. In addition to the standard few-shot task adaptation, we also consider the more challenging multi-domain task adaptation and few-shot dataset generalization settings in our empirical studies. Our results shows that CAML consistently outperforms best known approaches and achieves improved generalization.

On Graph Neural Network Fairness in the Presence of Heterophilous Neighborhoods

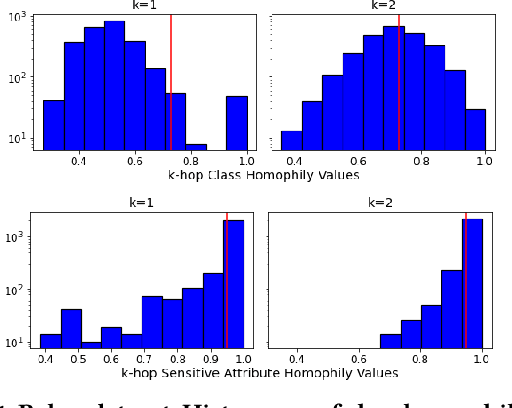
We study the task of node classification for graph neural networks (GNNs) and establish a connection between group fairness, as measured by statistical parity and equal opportunity, and local assortativity, i.e., the tendency of linked nodes to have similar attributes. Such assortativity is often induced by homophily, the tendency for nodes of similar properties to connect. Homophily can be common in social networks where systemic factors have forced individuals into communities which share a sensitive attribute. Through synthetic graphs, we study the interplay between locally occurring homophily and fair predictions, finding that not all node neighborhoods are equal in this respect -- neighborhoods dominated by one category of a sensitive attribute often struggle to obtain fair treatment, especially in the case of diverging local class and sensitive attribute homophily. After determining that a relationship between local homophily and fairness exists, we investigate if the issue of unfairness can be associated to the design of the applied GNN model. We show that by adopting heterophilous GNN designs capable of handling disassortative group labels, group fairness in locally heterophilous neighborhoods can be improved by up to 25% over homophilous designs in real and synthetic datasets.

Emerging Patterns in the Continuum Representation of Protein-Lipid Fingerprints

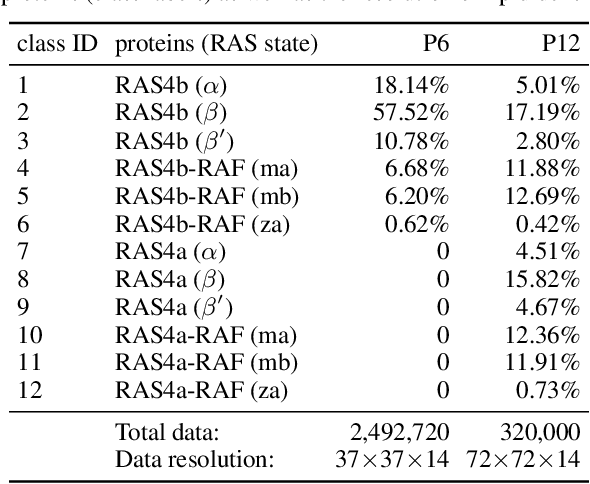
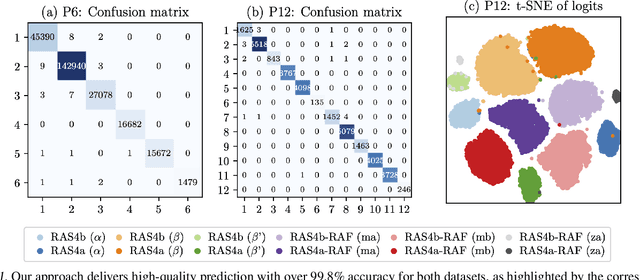
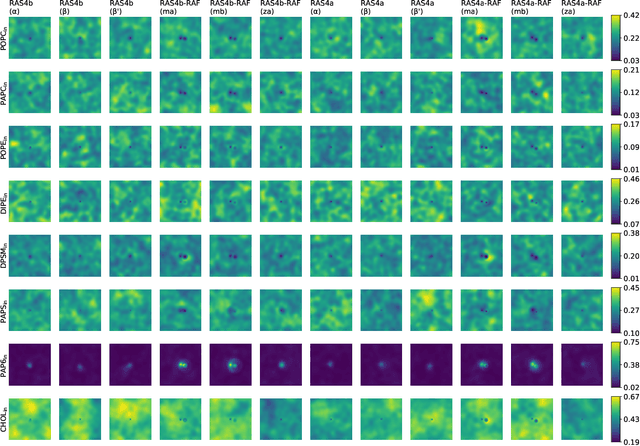
Capturing intricate biological phenomena often requires multiscale modeling where coarse and inexpensive models are developed using limited components of expensive and high-fidelity models. Here, we consider such a multiscale framework in the context of cancer biology and address the challenge of evaluating the descriptive capabilities of a continuum model developed using 1-dimensional statistics from a molecular dynamics model. Using deep learning, we develop a highly predictive classification model that identifies complex and emergent behavior from the continuum model. With over 99.9% accuracy demonstrated for two simulations, our approach confirms the existence of protein-specific "lipid fingerprints", i.e. spatial rearrangements of lipids in response to proteins of interest. Through this demonstration, our model also provides external validation of the continuum model, affirms the value of such multiscale modeling, and can foster new insights through further analysis of these fingerprints.

Node Proximity Is All You Need: Unified Structural and Positional Node and Graph Embedding

While most network embedding techniques model the relative positions of nodes in a network, recently there has been significant interest in structural embeddings that model node role equivalences, irrespective of their distances to any specific nodes. We present PhUSION, a proximity-based unified framework for computing structural and positional node embeddings, which leverages well-established methods for calculating node proximity scores. Clarifying a point of contention in the literature, we show which step of PhUSION produces the different kinds of embeddings and what steps can be used by both. Moreover, by aggregating the PhUSION node embeddings, we obtain graph-level features that model information lost by previous graph feature learning and kernel methods. In a comprehensive empirical study with over 10 datasets, 4 tasks, and 35 methods, we systematically reveal successful design choices for node and graph-level machine learning with embeddings.

G-CREWE: Graph CompREssion With Embedding for Network Alignment

Network alignment is useful for multiple applications that require increasingly large graphs to be processed. Existing research approaches this as an optimization problem or computes the similarity based on node representations. However, the process of aligning every pair of nodes between relatively large networks is time-consuming and resource-intensive. In this paper, we propose a framework, called G-CREWE (Graph CompREssion With Embedding) to solve the network alignment problem. G-CREWE uses node embeddings to align the networks on two levels of resolution, a fine resolution given by the original network and a coarse resolution given by a compressed version, to achieve an efficient and effective network alignment. The framework first extracts node features and learns the node embedding via a Graph Convolutional Network (GCN). Then, node embedding helps to guide the process of graph compression and finally improve the alignment performance. As part of G-CREWE, we also propose a new compression mechanism called MERGE (Minimum dEgRee neiGhbors comprEssion) to reduce the size of the input networks while preserving the consistency in their topological structure. Experiments on all real networks show that our method is more than twice as fast as the most competitive existing methods while maintaining high accuracy.

Generalizing Graph Neural Networks Beyond Homophily

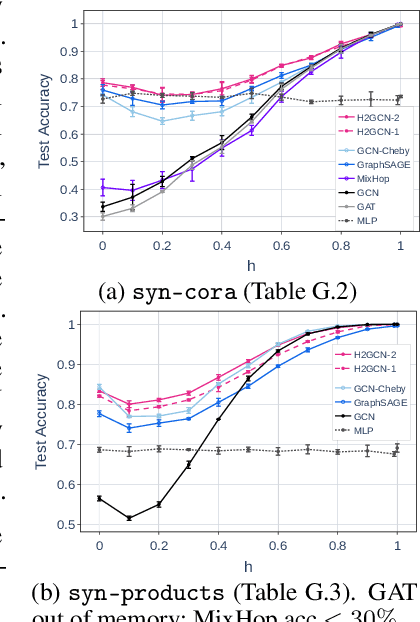
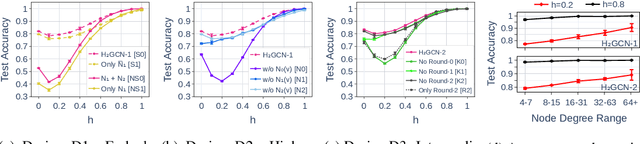
We investigate the representation power of graph neural networks in the semi-supervised node classification task under heterophily or low homophily, i.e., in networks where connected nodes may have different class labels and dissimilar features. Most existing GNNs fail to generalize to this setting, and are even outperformed by models that ignore the graph structure (e.g., multilayer perceptrons). Motivated by this limitation, we identify a set of key designs -- ego- and neighbor-embedding separation, higher-order neighborhoods, and combination of intermediate representations -- that boost learning from the graph structure under heterophily, and combine them into a new graph convolutional neural network, H2GCN. Going beyond the traditional benchmarks with strong homophily, our empirical analysis on synthetic and real networks shows that, thanks to the identified designs, H2GCN has consistently strong performance across the full spectrum of low-to-high homophily, unlike competitive prior models without them.