On Performance Discrepancies Across Local Homophily Levels in Graph Neural Networks

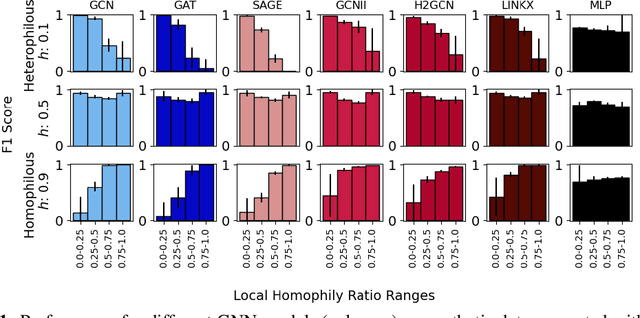
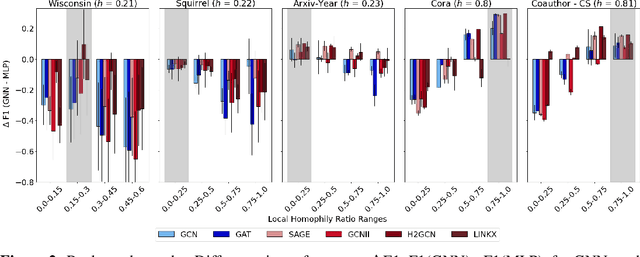
Research on GNNs has highlighted a relationship between high homophily (i.e., the tendency for nodes of a similar class to connect) and strong predictive performance in node classification. However, recent research has found the relationship to be more nuanced, demonstrating that even simple GNNs can learn in certain heterophilous settings. To bridge the gap between these findings, we revisit the assumptions made in previous works and identify that datasets are often treated as having a constant homophily level across nodes. To align closer to real-world datasets, we theoretically and empirically study the performance of GNNs when the local homophily level of a node deviates at test-time from the global homophily level of its graph. To aid our theoretical analysis, we introduce a new parameter to the preferential attachment model commonly used in homophily analysis to enable the control of local homophily levels in generated graphs, enabling a systematic empirical study on how local homophily can impact performance. We additionally perform a granular analysis on a number of real-world datasets with varying global homophily levels. Across our theoretical and empirical results, we find that (a)~ GNNs can fail to generalize to test nodes that deviate from the global homophily of a graph, (b)~ high local homophily does not necessarily confer high performance for a node, and (c)~ GNN models designed to handle heterophily are able to perform better across varying heterophily ranges irrespective of the dataset's global homophily. These findings point towards a GNN's over-reliance on the global homophily used for training and motivates the need to design GNNs that can better generalize across large local homophily ranges.

It's Not Fairness, and It's Not Fair: The Failure of Distributional Equality and the Promise of Relational Equality in Complete-Information Hiring Games

Existing efforts to formulate computational definitions of fairness have largely focused on distributional notions of equality, where equality is defined by the resources or decisions given to individuals in the system. Yet existing discrimination and injustice is often the result of unequal social relations, rather than an unequal distribution of resources. Here, we show how optimizing for existing computational and economic definitions of fairness and equality fail to prevent unequal social relations. To do this, we provide an example of a self-confirming equilibrium in a simple hiring market that is relationally unequal but satisfies existing distributional notions of fairness. In doing so, we introduce a notion of blatant relational unfairness for complete-information games, and discuss how this definition helps initiate a new approach to incorporating relational equality into computational systems.

On the Complexity of Learning from Label Proportions

In the problem of learning with label proportions, which we call LLP learning, the training data is unlabeled, and only the proportions of examples receiving each label are given. The goal is to learn a hypothesis that predicts the proportions of labels on the distribution underlying the sample. This model of learning is applicable to a wide variety of settings, including predicting the number of votes for candidates in political elections from polls. In this paper, we formally define this class and resolve foundational questions regarding the computational complexity of LLP and characterize its relationship to PAC learning. Among our results, we show, perhaps surprisingly, that for finite VC classes what can be efficiently LLP learned is a strict subset of what can be leaned efficiently in PAC, under standard complexity assumptions. We also show that there exist classes of functions whose learnability in LLP is independent of ZFC, the standard set theoretic axioms. This implies that LLP learning cannot be easily characterized (like PAC by VC dimension).

Sublinear-Time Adaptive Data Analysis

The central aim of most fields of data analysis and experimental scientific investigation is to draw valid conclusions from a given data set. But when past inferences guide future inquiries into the same dataset, reaching valid inferences becomes significantly more difficult. In addition to avoiding the overfitting that can result from adaptive analysis, a data analyst often wants to use as little time and data as possible. A recent line of work in the theory community has established mechanisms that provide low generalization error on adaptive queries, yet there remain large gaps between established theoretical results and how data analysis is done in practice. Many practitioners, for instance, successfully employ bootstrapping and related sampling approaches in order to maintain validity and speed up analysis, but prior to this work, no theoretical analysis existed to justify employing such techniques in this adaptive setting. In this paper, we show how these techniques can be used to provably guarantee validity while speeding up analysis. Through this investigation, we initiate the study of sub-linear time mechanisms to answer adaptive queries into datasets. Perhaps surprisingly, we describe mechanisms that provide an exponential speed-up per query over previous mechanisms, without needing to increase the total amount of data needed for low generalization error. We also provide a method for achieving statistically-meaningful responses even when the mechanism is only allowed to see a constant number of samples from the data per query.

A supervised approach to time scale detection in dynamic networks

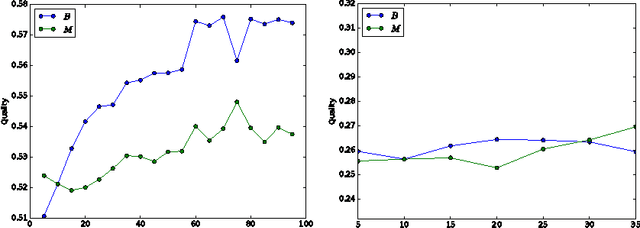
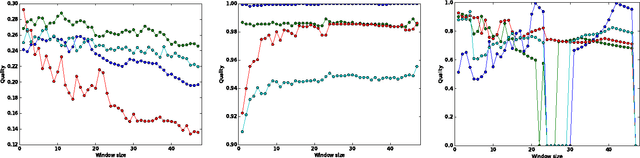
For any stream of time-stamped edges that form a dynamic network, an important choice is the aggregation granularity that an analyst uses to bin the data. Picking such a windowing of the data is often done by hand, or left up to the technology that is collecting the data. However, the choice can make a big difference in the properties of the dynamic network. This is the time scale detection problem. In previous work, this problem is often solved with a heuristic as an unsupervised task. As an unsupervised problem, it is difficult to measure how well a given algorithm performs. In addition, we show that the quality of the windowing is dependent on which task an analyst wants to perform on the network after windowing. Therefore the time scale detection problem should not be handled independently from the rest of the analysis of the network. We introduce a framework that tackles both of these issues: By measuring the performance of the time scale detection algorithm based on how well a given task is accomplished on the resulting network, we are for the first time able to directly compare different time scale detection algorithms to each other. Using this framework, we introduce time scale detection algorithms that take a supervised approach: they leverage ground truth on training data to find a good windowing of the test data. We compare the supervised approach to previous approaches and several baselines on real data.

A Confidence-Based Approach for Balancing Fairness and Accuracy

We study three classical machine learning algorithms in the context of algorithmic fairness: adaptive boosting, support vector machines, and logistic regression. Our goal is to maintain the high accuracy of these learning algorithms while reducing the degree to which they discriminate against individuals because of their membership in a protected group. Our first contribution is a method for achieving fairness by shifting the decision boundary for the protected group. The method is based on the theory of margins for boosting. Our method performs comparably to or outperforms previous algorithms in the fairness literature in terms of accuracy and low discrimination, while simultaneously allowing for a fast and transparent quantification of the trade-off between bias and error. Our second contribution addresses the shortcomings of the bias-error trade-off studied in most of the algorithmic fairness literature. We demonstrate that even hopelessly naive modifications of a biased algorithm, which cannot be reasonably said to be fair, can still achieve low bias and high accuracy. To help to distinguish between these naive algorithms and more sensible algorithms we propose a new measure of fairness, called resilience to random bias (RRB). We demonstrate that RRB distinguishes well between our naive and sensible fairness algorithms. RRB together with bias and accuracy provides a more complete picture of the fairness of an algorithm.

Handling oversampling in dynamic networks using link prediction

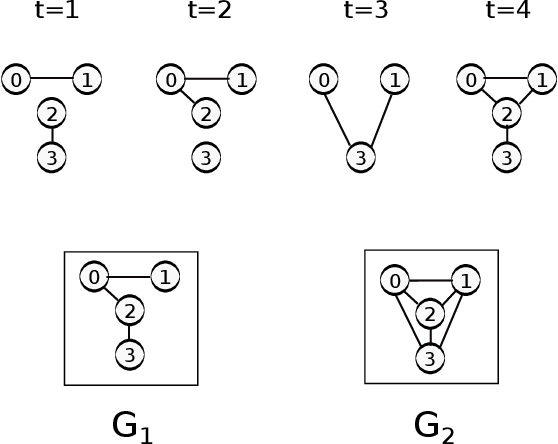
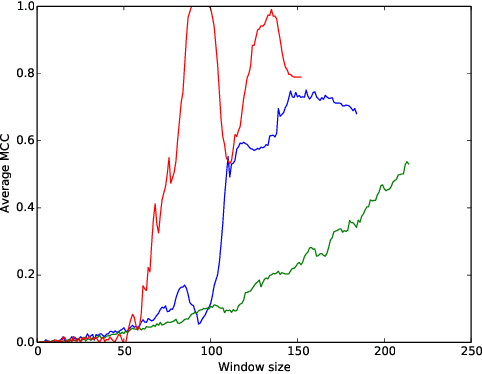
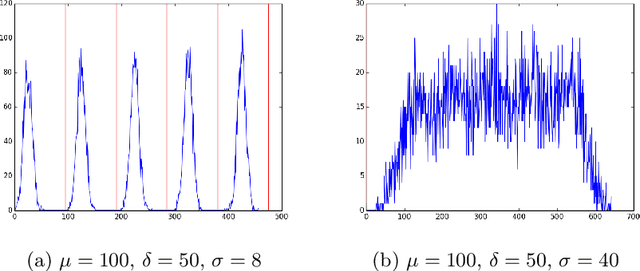
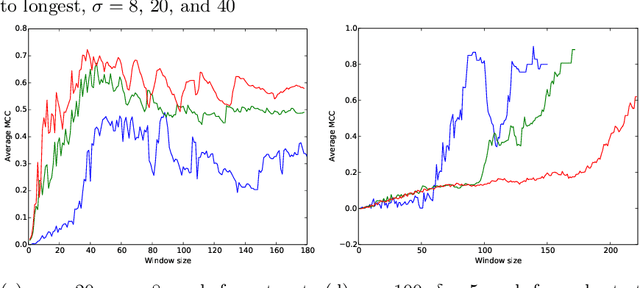
Oversampling is a common characteristic of data representing dynamic networks. It introduces noise into representations of dynamic networks, but there has been little work so far to compensate for it. Oversampling can affect the quality of many important algorithmic problems on dynamic networks, including link prediction. Link prediction seeks to predict edges that will be added to the network given previous snapshots. We show that not only does oversampling affect the quality of link prediction, but that we can use link prediction to recover from the effects of oversampling. We also introduce a novel generative model of noise in dynamic networks that represents oversampling. We demonstrate the results of our approach on both synthetic and real-world data.