Analyzing Data-Centric Properties for Contrastive Learning on Graphs

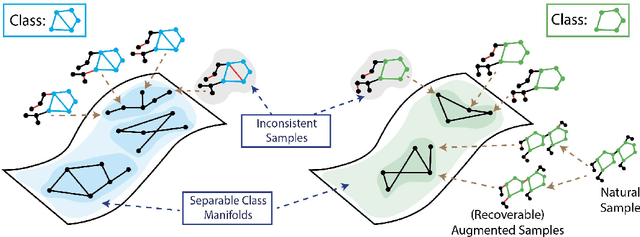
Recent analyses of self-supervised learning (SSL) find the following data-centric properties to be critical for learning good representations: invariance to task-irrelevant semantics, separability of classes in some latent space, and recoverability of labels from augmented samples. However, given their discrete, non-Euclidean nature, graph datasets and graph SSL methods are unlikely to satisfy these properties. This raises the question: how do graph SSL methods, such as contrastive learning (CL), work well? To systematically probe this question, we perform a generalization analysis for CL when using generic graph augmentations (GGAs), with a focus on data-centric properties. Our analysis yields formal insights into the limitations of GGAs and the necessity of task-relevant augmentations. As we empirically show, GGAs do not induce task-relevant invariances on common benchmark datasets, leading to only marginal gains over naive, untrained baselines. Our theory motivates a synthetic data generation process that enables control over task-relevant information and boasts pre-defined optimal augmentations. This flexible benchmark helps us identify yet unrecognized limitations in advanced augmentation techniques (e.g., automated methods). Overall, our work rigorously contextualizes, both empirically and theoretically, the effects of data-centric properties on augmentation strategies and learning paradigms for graph SSL.