Relational Causal Discovery with Latent Confounders

Estimating causal effects from real-world relational data can be challenging when the underlying causal model and potential confounders are unknown. While several causal discovery algorithms exist for learning causal models with latent confounders from data, they assume that the data is independent and identically distributed (i.i.d.) and are not well-suited for learning from relational data. Similarly, existing relational causal discovery algorithms assume causal sufficiency, which is unrealistic for many real-world datasets. To address this gap, we propose RelFCI, a sound and complete causal discovery algorithm for relational data with latent confounders. Our work builds upon the Fast Causal Inference (FCI) and Relational Causal Discovery (RCD) algorithms and it defines new graphical models, necessary to support causal discovery in relational domains. We also establish soundness and completeness guarantees for relational d-separation with latent confounders. We present experimental results demonstrating the effectiveness of RelFCI in identifying the correct causal structure in relational causal models with latent confounders.

Learning Relational Causal Models with Cycles through Relational Acyclification

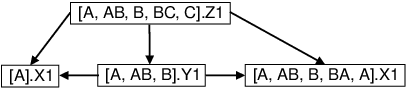
In real-world phenomena which involve mutual influence or causal effects between interconnected units, equilibrium states are typically represented with cycles in graphical models. An expressive class of graphical models, \textit{relational causal models}, can represent and reason about complex dynamic systems exhibiting such cycles or feedback loops. Existing cyclic causal discovery algorithms for learning causal models from observational data assume that the data instances are independent and identically distributed which makes them unsuitable for relational causal models. At the same time, causal discovery algorithms for relational causal models assume acyclicity. In this work, we examine the necessary and sufficient conditions under which a constraint-based relational causal discovery algorithm is sound and complete for \textit{cyclic relational causal models}. We introduce \textit{relational acyclification}, an operation specifically designed for relational models that enables reasoning about the identifiability of cyclic relational causal models. We show that under the assumptions of relational acyclification and $\sigma$-faithfulness, the relational causal discovery algorithm RCD (Maier et al. 2013) is sound and complete for cyclic models. We present experimental results to support our claim.

Non-Parametric Inference of Relational Dependence

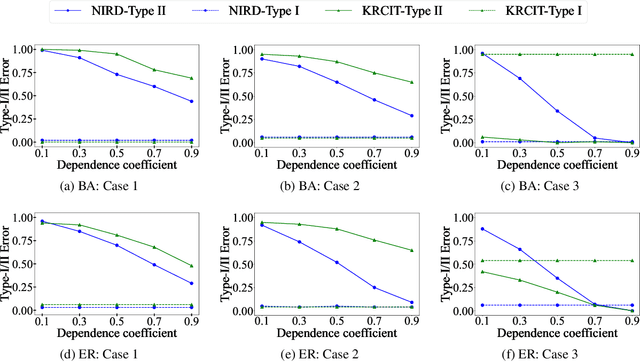
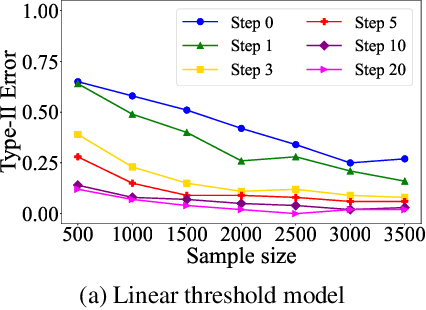
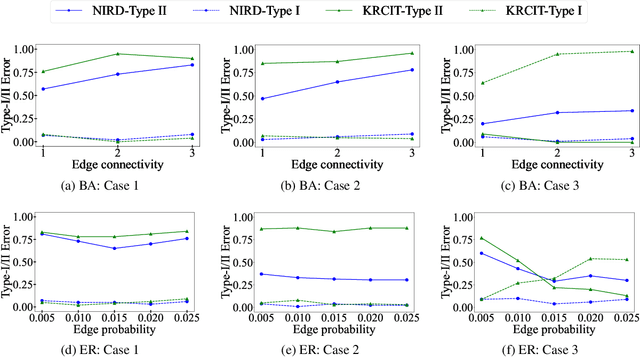
Independence testing plays a central role in statistical and causal inference from observational data. Standard independence tests assume that the data samples are independent and identically distributed (i.i.d.) but that assumption is violated in many real-world datasets and applications centered on relational systems. This work examines the problem of estimating independence in data drawn from relational systems by defining sufficient representations for the sets of observations influencing individual instances. Specifically, we define marginal and conditional independence tests for relational data by considering the kernel mean embedding as a flexible aggregation function for relational variables. We propose a consistent, non-parametric, scalable kernel test to operationalize the relational independence test for non-i.i.d. observational data under a set of structural assumptions. We empirically evaluate our proposed method on a variety of synthetic and semi-synthetic networks and demonstrate its effectiveness compared to state-of-the-art kernel-based independence tests.

Relational Causal Models with Cycles:Representation and Reasoning

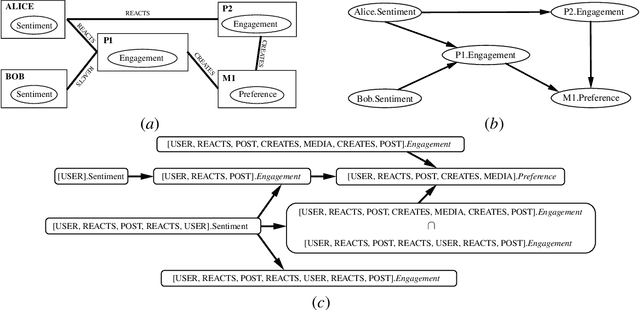
Causal reasoning in relational domains is fundamental to studying real-world social phenomena in which individual units can influence each other's traits and behavior. Dynamics between interconnected units can be represented as an instantiation of a relational causal model; however, causal reasoning over such instantiation requires additional templating assumptions that capture feedback loops of influence. Previous research has developed lifted representations to address the relational nature of such dynamics but has strictly required that the representation has no cycles. To facilitate cycles in relational representation and learning, we introduce relational $\sigma$-separation, a new criterion for understanding relational systems with feedback loops. We also introduce a new lifted representation, $\sigma$-abstract ground graph which helps with abstracting statistical independence relations in all possible instantiations of the cyclic relational model. We show the necessary and sufficient conditions for the completeness of $\sigma$-AGG and that relational $\sigma$-separation is sound and complete in the presence of one or more cycles with arbitrary length. To the best of our knowledge, this is the first work on representation of and reasoning with cyclic relational causal models.