Efficient Algorithms for Computing Random Walk Centrality

Random walk centrality is a fundamental metric in graph mining for quantifying node importance and influence, defined as the weighted average of hitting times to a node from all other nodes. Despite its ability to capture rich graph structural information and its wide range of applications, computing this measure for large networks remains impractical due to the computational demands of existing methods. In this paper, we present a novel formulation of random walk centrality, underpinning two scalable algorithms: one leveraging approximate Cholesky factorization and sparse inverse estimation, while the other sampling rooted spanning trees. Both algorithms operate in near-linear time and provide strong approximation guarantees. Extensive experiments on large real-world networks, including one with over 10 million nodes, demonstrate the efficiency and approximation quality of the proposed algorithms.

Graph-based Fake Account Detection: A Survey

In recent years, there has been a growing effort to develop effective and efficient algorithms for fake account detection in online social networks. This survey comprehensively reviews existing methods, with a focus on graph-based techniques that utilise topological features of social graphs (in addition to account information, such as their shared contents and profile data) to distinguish between fake and real accounts. We provide several categorisations of these methods (for example, based on techniques used, input data, and detection time), discuss their strengths and limitations, and explain how these methods connect in the broader context. We also investigate the available datasets, including both real-world data and synthesised models. We conclude the paper by proposing several potential avenues for future research.

Depth-Adaptive Graph Neural Networks via Learnable Bakry-'Emery Curvature

Graph Neural Networks (GNNs) have demonstrated strong representation learning capabilities for graph-based tasks. Recent advances on GNNs leverage geometric properties, such as curvature, to enhance its representation capabilities by modeling complex connectivity patterns and information flow within graphs. However, most existing approaches focus solely on discrete graph topology, overlooking diffusion dynamics and task-specific dependencies essential for effective learning. To address this, we propose integrating Bakry-\'Emery curvature, which captures both structural and task-driven aspects of information propagation. We develop an efficient, learnable approximation strategy, making curvature computation scalable for large graphs. Furthermore, we introduce an adaptive depth mechanism that dynamically adjusts message-passing layers per vertex based on its curvature, ensuring efficient propagation. Our theoretical analysis establishes a link between curvature and feature distinctiveness, showing that high-curvature vertices require fewer layers, while low-curvature ones benefit from deeper propagation. Extensive experiments on benchmark datasets validate the effectiveness of our approach, showing consistent performance improvements across diverse graph learning tasks.

DeepSN: A Sheaf Neural Framework for Influence Maximization

Influence maximization is key topic in data mining, with broad applications in social network analysis and viral marketing. In recent years, researchers have increasingly turned to machine learning techniques to address this problem. They have developed methods to learn the underlying diffusion processes in a data-driven manner, which enhances the generalizability of the solution, and have designed optimization objectives to identify the optimal seed set. Nonetheless, two fundamental gaps remain unsolved: (1) Graph Neural Networks (GNNs) are increasingly used to learn diffusion models, but in their traditional form, they often fail to capture the complex dynamics of influence diffusion, (2) Designing optimization objectives is challenging due to combinatorial explosion when solving this problem. To address these challenges, we propose a novel framework, DeepSN. Our framework employs sheaf neural diffusion to learn diverse influence patterns in a data-driven, end-to-end manner, providing enhanced separability in capturing diffusion characteristics. We also propose an optimization technique that accounts for overlapping influence between vertices, which helps to reduce the search space and identify the optimal seed set effectively and efficiently. Finally, we conduct extensive experiments on both synthetic and real-world datasets to demonstrate the effectiveness of our framework.

A Generalisation of Voter Model: Influential Nodes and Convergence Properties

Consider an undirected graph G, representing a social network, where each node is blue or red, corresponding to positive or negative opinion on a topic. In the voter model, in discrete time rounds, each node picks a neighbour uniformly at random and adopts its colour. Despite its significant popularity, this model does not capture some fundamental real-world characteristics such as the difference in the strengths of individuals connections, individuals with neutral opinion on a topic, and individuals who are reluctant to update their opinion. To address these issues, we introduce and study a generalisation of the voter model. Motivating by campaigning strategies, we study the problem of selecting a set of seeds blue nodes to maximise the expected number of blue nodes after some rounds. We prove that the problem is NP- hard and provide a polynomial time approximation algorithm with the best possible approximation guarantee. Our experiments on real-world and synthetic graph data demonstrate that the proposed algorithm outperforms other algorithms. We also investigate the convergence properties of the model. We prove that the process could take an exponential number of rounds to converge. However, if we limit ourselves to strongly connected graphs, the convergence time is polynomial and the period (the number of states in convergence) divides the length of all cycles in the graph.

A First Principles Approach to Trust-Based Recommendation Systems

This paper explores recommender systems in social networks which leverage information such as item rating, intra-item similarities, and trust graph. We demonstrate that item-rating information is more influential than other information types in a collaborative filtering approach. The trust graph-based approaches were found to be more robust to network adversarial attacks due to hard-to-manipulate trust structures. Intra-item information, although sub-optimal in isolation, enhances the consistency of predictions and lower-end performance when fused with other information forms. Additionally, the Weighted Average framework is introduced, enabling the construction of recommendation systems around any user-to-user similarity metric.

Viral Marketing in Social Networks with Competing Products

Consider a directed network where each node is either red (using the red product), blue (using the blue product), or uncolored (undecided). Then in each round, an uncolored node chooses red (resp. blue) with some probability proportional to the number of its red (resp. blue) out-neighbors. What is the best strategy to maximize the expected final number of red nodes given the budget to select $k$ red seed nodes? After proving that this problem is computationally hard, we provide a polynomial time approximation algorithm with the best possible approximation guarantee, building on the monotonicity and submodularity of the objective function and exploiting the Monte Carlo method. Furthermore, our experiments on various real-world and synthetic networks demonstrate that our proposed algorithm outperforms other algorithms. Additionally, we investigate the convergence time of the aforementioned process both theoretically and experimentally. In particular, we prove several tight bounds on the convergence time in terms of different graph parameters, such as the number of nodes/edges, maximum out-degree and diameter, by developing novel proof techniques.

A Fast Algorithm for Moderating Critical Nodes via Edge Removal

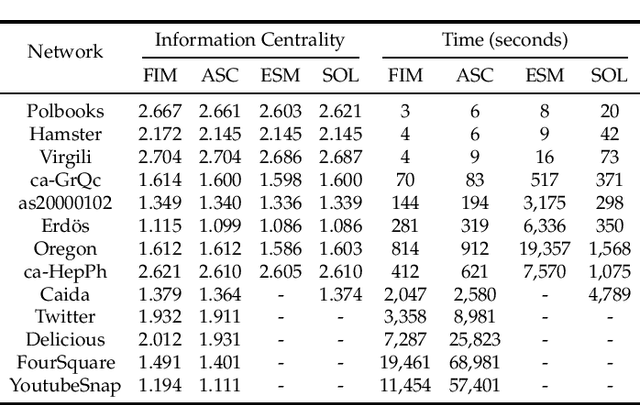
Critical nodes in networks are extremely vulnerable to malicious attacks to trigger negative cascading events such as the spread of misinformation and diseases. Therefore, effective moderation of critical nodes is very vital for mitigating the potential damages caused by such malicious diffusions. The current moderation methods are computationally expensive. Furthermore, they disregard the fundamental metric of information centrality, which measures the dissemination power of nodes. We investigate the problem of removing $k$ edges from a network to minimize the information centrality of a target node $\lea$ while preserving the network's connectivity. We prove that this problem is computationally challenging: it is NP-complete and its objective function is not supermodular. However, we propose three approximation greedy algorithms using novel techniques such as random walk-based Schur complement approximation and fast sum estimation. One of our algorithms runs in nearly linear time in the number of edges. To complement our theoretical analysis, we conduct a comprehensive set of experiments on synthetic and real networks with over one million nodes. Across various settings, the experimental results illustrate the effectiveness and efficiency of our proposed algorithms.

Random Majority Opinion Diffusion: Stabilization Time, Absorbing States, and Influential Nodes

Consider a graph G with n nodes and m edges, which represents a social network, and assume that initially each node is blue or white. In each round, all nodes simultaneously update their color to the most frequent color in their neighborhood. This is called the Majority Model (MM) if a node keeps its color in case of a tie and the Random Majority Model (RMM) if it chooses blue with probability 1/2 and white otherwise. We prove that there are graphs for which RMM needs exponentially many rounds to reach a stable configuration in expectation, and such a configuration can have exponentially many states (i.e., colorings). This is in contrast to MM, which is known to always reach a stable configuration with one or two states in $O(m)$ rounds. For the special case of a cycle graph C_n, we prove the stronger and tight bounds of $\lceil n/2\rceil-1$ and $O(n^2)$ in MM and RMM, respectively. Furthermore, we show that the number of stable colorings in MM on C_n is equal to $\Theta(\Phi^n)$, where $\Phi = (1+\sqrt{5})/2$ is the golden ratio, while it is equal to 2 for RMM. We also study the minimum size of a winning set, which is a set of nodes whose agreement on a color in the initial coloring enforces the process to end in a coloring where all nodes share that color. We present tight bounds on the minimum size of a winning set for both MM and RMM. Furthermore, we analyze our models for a random initial coloring, where each node is colored blue independently with some probability $p$ and white otherwise. Using some martingale analysis and counting arguments, we prove that the expected final number of blue nodes is respectively equal to $(2p^2-p^3)n/(1-p+p^2)$ and pn in MM and RMM on a cycle graph C_n. Finally, we conduct some experiments which complement our theoretical findings and also lead to the proposal of some intriguing open problems and conjectures to be tackled in future work.

On the Oracle Complexity of Higher-Order Smooth Non-Convex Finite-Sum Optimization

We prove lower bounds for higher-order methods in smooth non-convex finite-sum optimization. Our contribution is threefold: We first show that a deterministic algorithm cannot profit from the finite-sum structure of the objective, and that simulating a pth-order regularized method on the whole function by constructing exact gradient information is optimal up to constant factors. We further show lower bounds for randomized algorithms and compare them with the best known upper bounds. To address some gaps between the bounds, we propose a new second-order smoothness assumption that can be seen as an analogue of the first-order mean-squared smoothness assumption. We prove that it is sufficient to ensure state-of-the-art convergence guarantees, while allowing for a sharper lower bound.