Promoting Fairness in Information Access within Social Networks

The advent of online social networks has facilitated fast and wide spread of information. However, some users, especially members of minority groups, may be less likely to receive information spreading on the network, due to their disadvantaged network position. We study the optimization problem of adding new connections to a network to enhance fairness in information access among different demographic groups. We provide a concrete formulation of this problem where information access is measured in terms of resistance distance, {offering a new perspective that emphasizes global network structure and multi-path connectivity.} The problem is shown to be NP-hard. We propose a simple greedy algorithm which turns out to output accurate solutions, but its run time is cubic, which makes it undesirable for large networks. As our main technical contribution, we reduce its time complexity to linear, leveraging several novel approximation techniques. In addition to our theoretical findings, we also conduct an extensive set of experiments using both real-world and synthetic datasets. We demonstrate that our linear-time algorithm can produce accurate solutions for networks with millions of nodes.

Efficient Algorithms for Computing Random Walk Centrality

Random walk centrality is a fundamental metric in graph mining for quantifying node importance and influence, defined as the weighted average of hitting times to a node from all other nodes. Despite its ability to capture rich graph structural information and its wide range of applications, computing this measure for large networks remains impractical due to the computational demands of existing methods. In this paper, we present a novel formulation of random walk centrality, underpinning two scalable algorithms: one leveraging approximate Cholesky factorization and sparse inverse estimation, while the other sampling rooted spanning trees. Both algorithms operate in near-linear time and provide strong approximation guarantees. Extensive experiments on large real-world networks, including one with over 10 million nodes, demonstrate the efficiency and approximation quality of the proposed algorithms.

Finding Influencers in Complex Networks: An Effective Deep Reinforcement Learning Approach

Maximizing influences in complex networks is a practically important but computationally challenging task for social network analysis, due to its NP- hard nature. Most current approximation or heuristic methods either require tremendous human design efforts or achieve unsatisfying balances between effectiveness and efficiency. Recent machine learning attempts only focus on speed but lack performance enhancement. In this paper, different from previous attempts, we propose an effective deep reinforcement learning model that achieves superior performances over traditional best influence maximization algorithms. Specifically, we design an end-to-end learning framework that combines graph neural network as the encoder and reinforcement learning as the decoder, named DREIM. Trough extensive training on small synthetic graphs, DREIM outperforms the state-of-the-art baseline methods on very large synthetic and real-world networks on solution quality, and we also empirically show its linear scalability with regard to the network size, which demonstrates its superiority in solving this problem.

A Fast Algorithm for Moderating Critical Nodes via Edge Removal

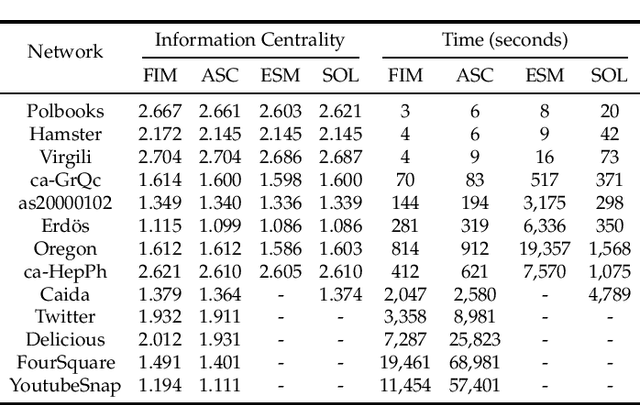
Critical nodes in networks are extremely vulnerable to malicious attacks to trigger negative cascading events such as the spread of misinformation and diseases. Therefore, effective moderation of critical nodes is very vital for mitigating the potential damages caused by such malicious diffusions. The current moderation methods are computationally expensive. Furthermore, they disregard the fundamental metric of information centrality, which measures the dissemination power of nodes. We investigate the problem of removing $k$ edges from a network to minimize the information centrality of a target node $\lea$ while preserving the network's connectivity. We prove that this problem is computationally challenging: it is NP-complete and its objective function is not supermodular. However, we propose three approximation greedy algorithms using novel techniques such as random walk-based Schur complement approximation and fast sum estimation. One of our algorithms runs in nearly linear time in the number of edges. To complement our theoretical analysis, we conduct a comprehensive set of experiments on synthetic and real networks with over one million nodes. Across various settings, the experimental results illustrate the effectiveness and efficiency of our proposed algorithms.