Fast, Provable Algorithms for Isotonic Regression in all $\ell_{p}$-norms
Paper and Code
Nov 11, 2015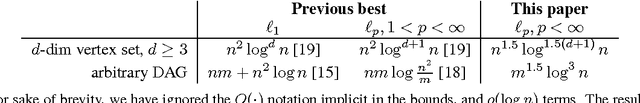
Given a directed acyclic graph $G,$ and a set of values $y$ on the vertices, the Isotonic Regression of $y$ is a vector $x$ that respects the partial order described by $G,$ and minimizes $||x-y||,$ for a specified norm. This paper gives improved algorithms for computing the Isotonic Regression for all weighted $\ell_{p}$-norms with rigorous performance guarantees. Our algorithms are quite practical, and their variants can be implemented to run fast in practice.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge