ADAGIO: Fast Data-aware Near-Isometric Linear Embeddings
Paper and Code
Sep 17, 2016
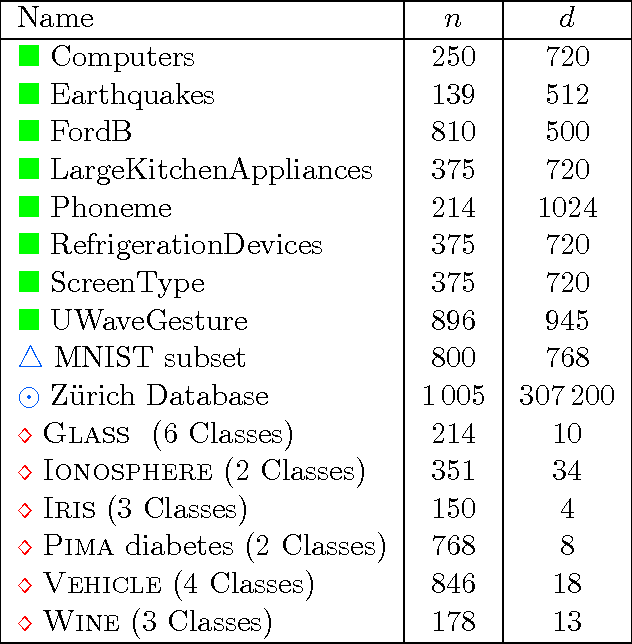
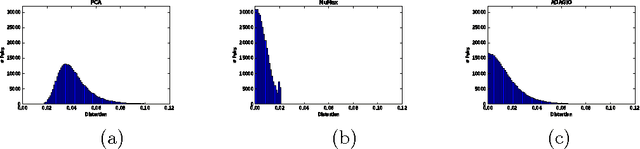

Many important applications, including signal reconstruction, parameter estimation, and signal processing in a compressed domain, rely on a low-dimensional representation of the dataset that preserves {\em all} pairwise distances between the data points and leverages the inherent geometric structure that is typically present. Recently Hedge, Sankaranarayanan, Yin and Baraniuk \cite{hedge2015} proposed the first data-aware near-isometric linear embedding which achieves the best of both worlds. However, their method NuMax does not scale to large-scale datasets. Our main contribution is a simple, data-aware, near-isometric linear dimensionality reduction method which significantly outperforms a state-of-the-art method \cite{hedge2015} with respect to scalability while achieving high quality near-isometries. Furthermore, our method comes with strong worst-case theoretical guarantees that allow us to guarantee the quality of the obtained near-isometry. We verify experimentally the efficiency of our method on numerous real-world datasets, where we find that our method ($<$10 secs) is more than 3\,000$\times$ faster than the state-of-the-art method \cite{hedge2015} ($>$9 hours) on medium scale datasets with 60\,000 data points in 784 dimensions. Finally, we use our method as a preprocessing step to increase the computational efficiency of a classification application and for speeding up approximate nearest neighbor queries.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge