An improved analysis of the ER-SpUD dictionary learning algorithm
Paper and Code
Feb 18, 2016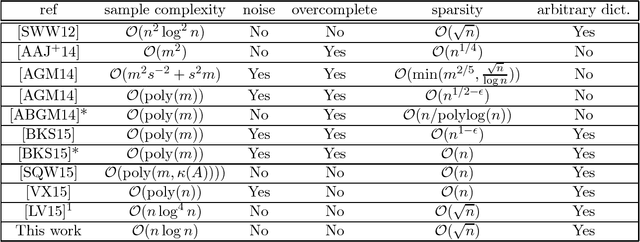

In "dictionary learning" we observe $Y = AX + E$ for some $Y\in\mathbb{R}^{n\times p}$, $A \in\mathbb{R}^{m\times n}$, and $X\in\mathbb{R}^{m\times p}$. The matrix $Y$ is observed, and $A, X, E$ are unknown. Here $E$ is "noise" of small norm, and $X$ is column-wise sparse. The matrix $A$ is referred to as a {\em dictionary}, and its columns as {\em atoms}. Then, given some small number $p$ of samples, i.e.\ columns of $Y$, the goal is to learn the dictionary $A$ up to small error, as well as $X$. The motivation is that in many applications data is expected to sparse when represented by atoms in the "right" dictionary $A$ (e.g.\ images in the Haar wavelet basis), and the goal is to learn $A$ from the data to then use it for other applications. Recently, [SWW12] proposed the dictionary learning algorithm ER-SpUD with provable guarantees when $E = 0$ and $m = n$. They showed if $X$ has independent entries with an expected $s$ non-zeroes per column for $1 \lesssim s \lesssim \sqrt{n}$, and with non-zero entries being subgaussian, then for $p\gtrsim n^2\log^2 n$ with high probability ER-SpUD outputs matrices $A', X'$ which equal $A, X$ up to permuting and scaling columns (resp.\ rows) of $A$ (resp.\ $X$). They conjectured $p\gtrsim n\log n$ suffices, which they showed was information theoretically necessary for {\em any} algorithm to succeed when $s \simeq 1$. Significant progress was later obtained in [LV15]. We show that for a slight variant of ER-SpUD, $p\gtrsim n\log(n/\delta)$ samples suffice for successful recovery with probability $1-\delta$. We also show that for the unmodified ER-SpUD, $p\gtrsim n^{1.99}$ samples are required even to learn $A, X$ with polynomially small success probability. This resolves the main conjecture of [SWW12], and contradicts the main result of [LV15], which claimed that $p\gtrsim n\log^4 n$ guarantees success whp.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge