Ben Lawson
Predicting Positive and Negative Links with Noisy Queries: Theory & Practice
Aug 07, 2018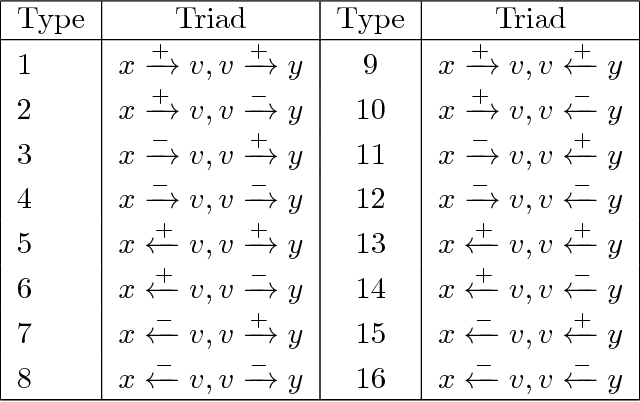

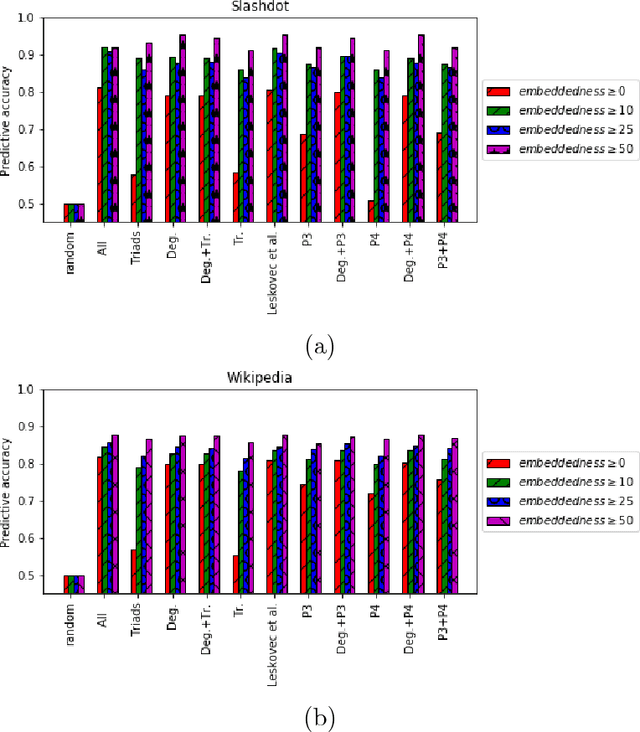
Abstract:Social networks involve both positive and negative relationships, which can be captured in signed graphs. The {\em edge sign prediction problem} aims to predict whether an interaction between a pair of nodes will be positive or negative. We provide theoretical results for this problem that motivate natural improvements to recent heuristics. The edge sign prediction problem is related to correlation clustering; a positive relationship means being in the same cluster. We consider the following model for two clusters: we are allowed to query any pair of nodes whether they belong to the same cluster or not, but the answer to the query is corrupted with some probability $0<q<\frac{1}{2}$. Let $\delta=1-2q$ be the bias. We provide an algorithm that recovers all signs correctly with high probability in the presence of noise with $O(\frac{n\log n}{\delta^2}+\frac{\log^2 n}{\delta^6})$ queries. This is the best known result for this problem for all but tiny $\delta$, improving on the recent work of Mazumdar and Saha \cite{mazumdar2017clustering}. We also provide an algorithm that performs $O(\frac{n\log n}{\delta^4})$ queries, and uses breadth first search as its main algorithmic primitive. While both the running time and the number of queries for this algorithm are sub-optimal, our result relies on novel theoretical techniques, and naturally suggests the use of edge-disjoint paths as a feature for predicting signs in online social networks. Correspondingly, we experiment with using edge disjoint $s-t$ paths of short length as a feature for predicting the sign of edge $(s,t)$ in real-world signed networks. Empirical findings suggest that the use of such paths improves the classification accuracy, especially for pairs of nodes with no common neighbors.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge