What You See is What You Get: Distributional Generalization for Algorithm Design in Deep Learning

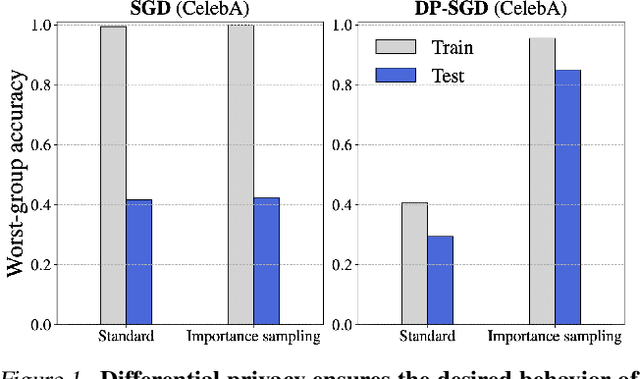
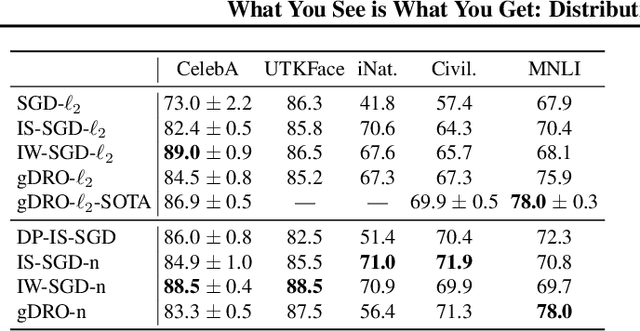
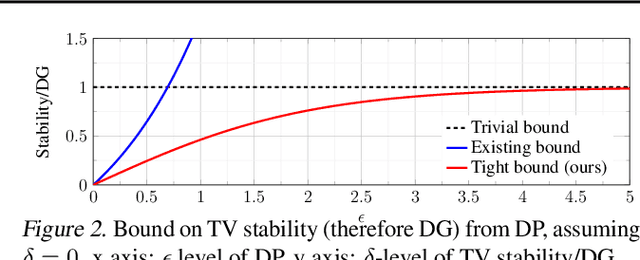
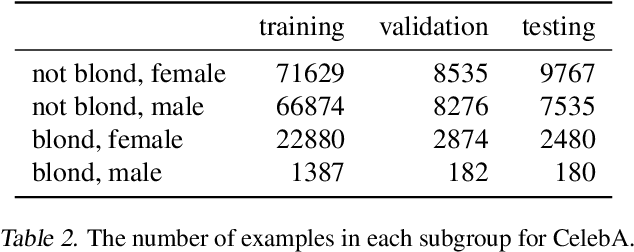
We investigate and leverage a connection between Differential Privacy (DP) and the recently proposed notion of Distributional Generalization (DG). Applying this connection, we introduce new conceptual tools for designing deep-learning methods that bypass "pathologies" of standard stochastic gradient descent (SGD). First, we prove that differentially private methods satisfy a "What You See Is What You Get (WYSIWYG)" generalization guarantee: whatever a model does on its train data is almost exactly what it will do at test time. This guarantee is formally captured by distributional generalization. WYSIWYG enables principled algorithm design in deep learning by reducing $\textit{generalization}$ concerns to $\textit{optimization}$ ones: in order to mitigate unwanted behavior at test time, it is provably sufficient to mitigate this behavior on the train data. This is notably false for standard (non-DP) methods, hence this observation has applications even when privacy is not required. For example, importance sampling is known to fail for standard SGD, but we show that it has exactly the intended effect for DP-trained models. Thus, with DP-SGD, unlike with SGD, we can influence test-time behavior by making principled train-time interventions. We use these insights to construct simple algorithms which match or outperform SOTA in several distributional robustness applications, and to significantly improve the privacy vs. disparate impact trade-off of DP-SGD. Finally, we also improve on known theoretical bounds relating differential privacy, stability, and distributional generalization.