Charlotte Peale
Representative Language Generation
May 27, 2025Abstract:We introduce "representative generation," extending the theoretical framework for generation proposed by Kleinberg et al. (2024) and formalized by Li et al. (2024), to additionally address diversity and bias concerns in generative models. Our notion requires outputs of a generative model to proportionally represent groups of interest from the training data. We characterize representative uniform and non-uniform generation, introducing the "group closure dimension" as a key combinatorial quantity. For representative generation in the limit, we analyze both information-theoretic and computational aspects, demonstrating feasibility for countably infinite hypothesis classes and collections of groups under certain conditions, but proving a negative result for computability using only membership queries. This contrasts with Kleinberg et al.'s (2024) positive results for standard generation in the limit. Our findings provide a rigorous foundation for developing more diverse and representative generative models.
When does a predictor know its own loss?
Feb 27, 2025Abstract:Given a predictor and a loss function, how well can we predict the loss that the predictor will incur on an input? This is the problem of loss prediction, a key computational task associated with uncertainty estimation for a predictor. In a classification setting, a predictor will typically predict a distribution over labels and hence have its own estimate of the loss that it will incur, given by the entropy of the predicted distribution. Should we trust this estimate? In other words, when does the predictor know what it knows and what it does not know? In this work we study the theoretical foundations of loss prediction. Our main contribution is to establish tight connections between nontrivial loss prediction and certain forms of multicalibration, a multigroup fairness notion that asks for calibrated predictions across computationally identifiable subgroups. Formally, we show that a loss predictor that is able to improve on the self-estimate of a predictor yields a witness to a failure of multicalibration, and vice versa. This has the implication that nontrivial loss prediction is in effect no easier or harder than auditing for multicalibration. We support our theoretical results with experiments that show a robust positive correlation between the multicalibration error of a predictor and the efficacy of training a loss predictor.
Provable Uncertainty Decomposition via Higher-Order Calibration
Dec 25, 2024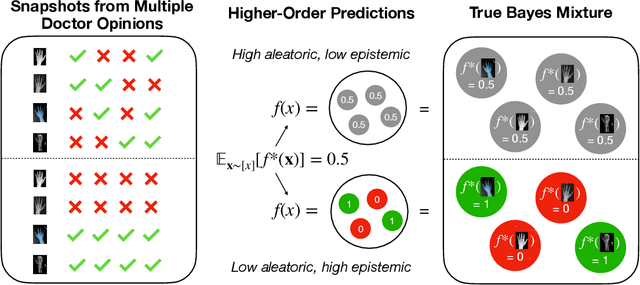
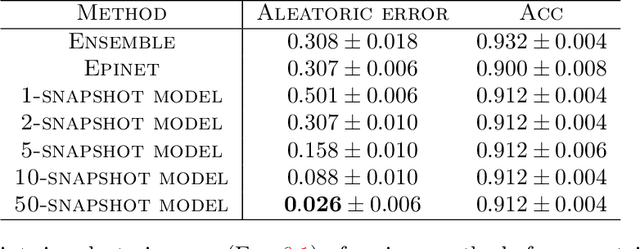
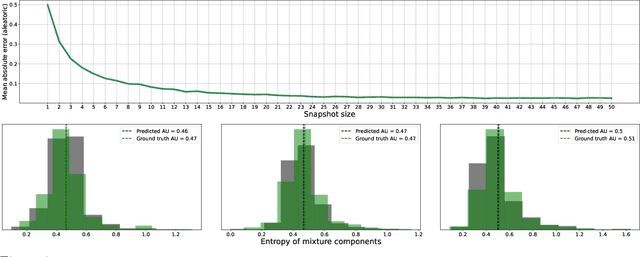
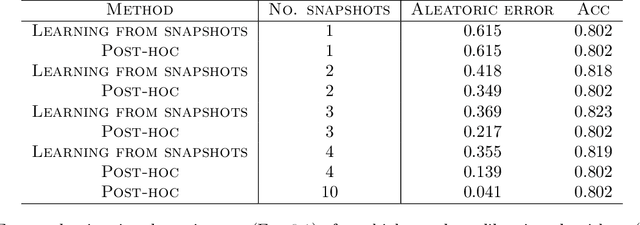
Abstract:We give a principled method for decomposing the predictive uncertainty of a model into aleatoric and epistemic components with explicit semantics relating them to the real-world data distribution. While many works in the literature have proposed such decompositions, they lack the type of formal guarantees we provide. Our method is based on the new notion of higher-order calibration, which generalizes ordinary calibration to the setting of higher-order predictors that predict mixtures over label distributions at every point. We show how to measure as well as achieve higher-order calibration using access to $k$-snapshots, namely examples where each point has $k$ independent conditional labels. Under higher-order calibration, the estimated aleatoric uncertainty at a point is guaranteed to match the real-world aleatoric uncertainty averaged over all points where the prediction is made. To our knowledge, this is the first formal guarantee of this type that places no assumptions whatsoever on the real-world data distribution. Importantly, higher-order calibration is also applicable to existing higher-order predictors such as Bayesian and ensemble models and provides a natural evaluation metric for such models. We demonstrate through experiments that our method produces meaningful uncertainty decompositions for image classification.
Taking a Moment for Distributional Robustness
May 08, 2024Abstract:A rich line of recent work has studied distributionally robust learning approaches that seek to learn a hypothesis that performs well, in the worst-case, on many different distributions over a population. We argue that although the most common approaches seek to minimize the worst-case loss over distributions, a more reasonable goal is to minimize the worst-case distance to the true conditional expectation of labels given each covariate. Focusing on the minmax loss objective can dramatically fail to output a solution minimizing the distance to the true conditional expectation when certain distributions contain high levels of label noise. We introduce a new min-max objective based on what is known as the adversarial moment violation and show that minimizing this objective is equivalent to minimizing the worst-case $\ell_2$-distance to the true conditional expectation if we take the adversary's strategy space to be sufficiently rich. Previous work has suggested minimizing the maximum regret over the worst-case distribution as a way to circumvent issues arising from differential noise levels. We show that in the case of square loss, minimizing the worst-case regret is also equivalent to minimizing the worst-case $\ell_2$-distance to the true conditional expectation. Although their objective and our objective both minimize the worst-case distance to the true conditional expectation, we show that our approach provides large empirical savings in computational cost in terms of the number of groups, while providing the same noise-oblivious worst-distribution guarantee as the minimax regret approach, thus making positive progress on an open question posed by Agarwal and Zhang (2022).
Multigroup Robustness
May 01, 2024Abstract:To address the shortcomings of real-world datasets, robust learning algorithms have been designed to overcome arbitrary and indiscriminate data corruption. However, practical processes of gathering data may lead to patterns of data corruption that are localized to specific partitions of the training dataset. Motivated by critical applications where the learned model is deployed to make predictions about people from a rich collection of overlapping subpopulations, we initiate the study of multigroup robust algorithms whose robustness guarantees for each subpopulation only degrade with the amount of data corruption inside that subpopulation. When the data corruption is not distributed uniformly over subpopulations, our algorithms provide more meaningful robustness guarantees than standard guarantees that are oblivious to how the data corruption and the affected subpopulations are related. Our techniques establish a new connection between multigroup fairness and robustness.
Comparative Learning: A Sample Complexity Theory for Two Hypothesis Classes
Nov 16, 2022Abstract:In many learning theory problems, a central role is played by a hypothesis class: we might assume that the data is labeled according to a hypothesis in the class (usually referred to as the realizable setting), or we might evaluate the learned model by comparing it with the best hypothesis in the class (the agnostic setting). Taking a step beyond these classic setups that involve only a single hypothesis class, we introduce comparative learning as a combination of the realizable and agnostic settings in PAC learning: given two binary hypothesis classes $S$ and $B$, we assume that the data is labeled according to a hypothesis in the source class $S$ and require the learned model to achieve an accuracy comparable to the best hypothesis in the benchmark class $B$. Even when both $S$ and $B$ have infinite VC dimensions, comparative learning can still have a small sample complexity. We show that the sample complexity of comparative learning is characterized by the mutual VC dimension $\mathsf{VC}(S,B)$ which we define to be the maximum size of a subset shattered by both $S$ and $B$. We also show a similar result in the online setting, where we give a regret characterization in terms of the mutual Littlestone dimension $\mathsf{Ldim}(S,B)$. These results also hold for partial hypotheses. We additionally show that the insights necessary to characterize the sample complexity of comparative learning can be applied to characterize the sample complexity of realizable multiaccuracy and multicalibration using the mutual fat-shattering dimension, an analogue of the mutual VC dimension for real-valued hypotheses. This not only solves an open problem proposed by Hu, Peale, Reingold (2022), but also leads to independently interesting results extending classic ones about regression, boosting, and covering number to our two-hypothesis-class setting.
Metric Entropy Duality and the Sample Complexity of Outcome Indistinguishability
Mar 09, 2022Abstract:We give the first sample complexity characterizations for outcome indistinguishability, a theoretical framework of machine learning recently introduced by Dwork, Kim, Reingold, Rothblum, and Yona (STOC 2021). In outcome indistinguishability, the goal of the learner is to output a predictor that cannot be distinguished from the target predictor by a class $D$ of distinguishers examining the outcomes generated according to the predictors' predictions. In the distribution-specific and realizable setting where the learner is given the data distribution together with a predictor class $P$ containing the target predictor, we show that the sample complexity of outcome indistinguishability is characterized by the metric entropy of $P$ w.r.t. the dual Minkowski norm defined by $D$, and equivalently by the metric entropy of $D$ w.r.t. the dual Minkowski norm defined by $P$. This equivalence makes an intriguing connection to the long-standing metric entropy duality conjecture in convex geometry. Our sample complexity characterization implies a variant of metric entropy duality, which we show is nearly tight. In the distribution-free setting, we focus on the case considered by Dwork et al. where $P$ contains all possible predictors, hence the sample complexity only depends on $D$. In this setting, we show that the sample complexity of outcome indistinguishability is characterized by the fat-shattering dimension of $D$. We also show a strong sample complexity separation between realizable and agnostic outcome indistinguishability in both the distribution-free and the distribution-specific settings. This is in contrast to distribution-free (resp. distribution-specific) PAC learning where the sample complexity in both the realizable and the agnostic settings can be characterized by the VC dimension (resp. metric entropy).
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge