Loss Minimization through the Lens of Outcome Indistinguishability

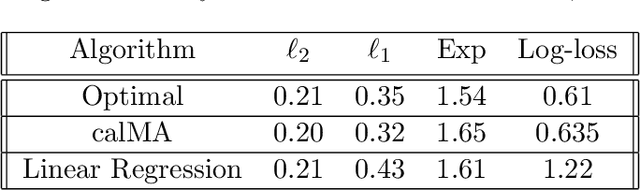
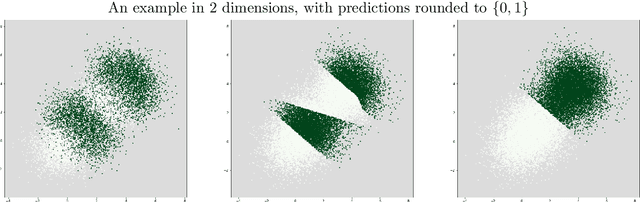
We present a new perspective on loss minimization and the recent notion of Omniprediction through the lens of Outcome Indistingusihability. For a collection of losses and hypothesis class, omniprediction requires that a predictor provide a loss-minimization guarantee simultaneously for every loss in the collection compared to the best (loss-specific) hypothesis in the class. We present a generic template to learn predictors satisfying a guarantee we call Loss Outcome Indistinguishability. For a set of statistical tests--based on a collection of losses and hypothesis class--a predictor is Loss OI if it is indistinguishable (according to the tests) from Nature's true probabilities over outcomes. By design, Loss OI implies omniprediction in a direct and intuitive manner. We simplify Loss OI further, decomposing it into a calibration condition plus multiaccuracy for a class of functions derived from the loss and hypothesis classes. By careful analysis of this class, we give efficient constructions of omnipredictors for interesting classes of loss functions, including non-convex losses. This decomposition highlights the utility of a new multi-group fairness notion that we call calibrated multiaccuracy, which lies in between multiaccuracy and multicalibration. We show that calibrated multiaccuracy implies Loss OI for the important set of convex losses arising from Generalized Linear Models, without requiring full multicalibration. For such losses, we show an equivalence between our computational notion of Loss OI and a geometric notion of indistinguishability, formulated as Pythagorean theorems in the associated Bregman divergence. We give an efficient algorithm for calibrated multiaccuracy with computational complexity comparable to that of multiaccuracy. In all, calibrated multiaccuracy offers an interesting tradeoff point between efficiency and generality in the omniprediction landscape.

KL Divergence Estimation with Multi-group Attribution

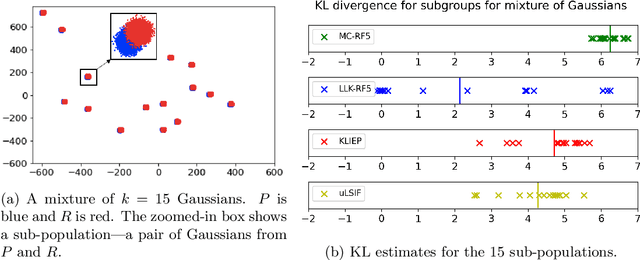
Estimating the Kullback-Leibler (KL) divergence between two distributions given samples from them is well-studied in machine learning and information theory. Motivated by considerations of multi-group fairness, we seek KL divergence estimates that accurately reflect the contributions of sub-populations to the overall divergence. We model the sub-populations coming from a rich (possibly infinite) family $\mathcal{C}$ of overlapping subsets of the domain. We propose the notion of multi-group attribution for $\mathcal{C}$, which requires that the estimated divergence conditioned on every sub-population in $\mathcal{C}$ satisfies some natural accuracy and fairness desiderata, such as ensuring that sub-populations where the model predicts significant divergence do diverge significantly in the two distributions. Our main technical contribution is to show that multi-group attribution can be derived from the recently introduced notion of multi-calibration for importance weights [HKRR18, GRSW21]. We provide experimental evidence to support our theoretical results, and show that multi-group attribution provides better KL divergence estimates when conditioned on sub-populations than other popular algorithms.

Omnipredictors

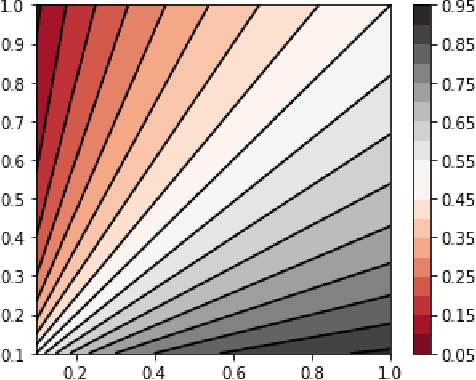
Loss minimization is a dominant paradigm in machine learning, where a predictor is trained to minimize some loss function that depends on an uncertain event (e.g., "will it rain tomorrow?''). Different loss functions imply different learning algorithms and, at times, very different predictors. While widespread and appealing, a clear drawback of this approach is that the loss function may not be known at the time of learning, requiring the algorithm to use a best-guess loss function. We suggest a rigorous new paradigm for loss minimization in machine learning where the loss function can be ignored at the time of learning and only be taken into account when deciding an action. We introduce the notion of an (${\mathcal{L}},\mathcal{C}$)-omnipredictor, which could be used to optimize any loss in a family ${\mathcal{L}}$. Once the loss function is set, the outputs of the predictor can be post-processed (a simple univariate data-independent transformation of individual predictions) to do well compared with any hypothesis from the class $\mathcal{C}$. The post processing is essentially what one would perform if the outputs of the predictor were true probabilities of the uncertain events. In a sense, omnipredictors extract all the predictive power from the class $\mathcal{C}$, irrespective of the loss function in $\mathcal{L}$. We show that such "loss-oblivious'' learning is feasible through a connection to multicalibration, a notion introduced in the context of algorithmic fairness. In addition, we show how multicalibration can be viewed as a solution concept for agnostic boosting, shedding new light on past results. Finally, we transfer our insights back to the context of algorithmic fairness by providing omnipredictors for multi-group loss minimization.

Multicalibrated Partitions for Importance Weights

The ratio between the probability that two distributions $R$ and $P$ give to points $x$ are known as importance weights or propensity scores and play a fundamental role in many different fields, most notably, statistics and machine learning. Among its applications, importance weights are central to domain adaptation, anomaly detection, and estimations of various divergences such as the KL divergence. We consider the common setting where $R$ and $P$ are only given through samples from each distribution. The vast literature on estimating importance weights is either heuristic, or makes strong assumptions about $R$ and $P$ or on the importance weights themselves. In this paper, we explore a computational perspective to the estimation of importance weights, which factors in the limitations and possibilities obtainable with bounded computational resources. We significantly strengthen previous work that use the MaxEntropy approach, that define the importance weights based on a distribution $Q$ closest to $P$, that looks the same as $R$ on every set $C \in \mathcal{C}$, where $\mathcal{C}$ may be a huge collection of sets. We show that the MaxEntropy approach may fail to assign high average scores to sets $C \in \mathcal{C}$, even when the average of ground truth weights for the set is evidently large. We similarly show that it may overestimate the average scores to sets $C \in \mathcal{C}$. We therefore formulate Sandwiching bounds as a notion of set-wise accuracy for importance weights. We study these bounds to show that they capture natural completeness and soundness requirements from the weights. We present an efficient algorithm that under standard learnability assumptions computes weights which satisfy these bounds. Our techniques rely on a new notion of multicalibrated partitions of the domain of the distributions, which appear to be useful objects in their own right.

PIDForest: Anomaly Detection via Partial Identification

We consider the problem of detecting anomalies in a large dataset. We propose a framework called Partial Identification which captures the intuition that anomalies are easy to distinguish from the overwhelming majority of points by relatively few attribute values. Formalizing this intuition, we propose a geometric anomaly measure for a point that we call PIDScore, which measures the minimum density of data points over all subcubes containing the point. We present PIDForest: a random forest based algorithm that finds anomalies based on this definition. We show that it performs favorably in comparison to several popular anomaly detection methods, across a broad range of benchmarks. PIDForest also provides a succinct explanation for why a point is labelled anomalous, by providing a set of features and ranges for them which are relatively uncommon in the dataset.

Faster Anomaly Detection via Matrix Sketching

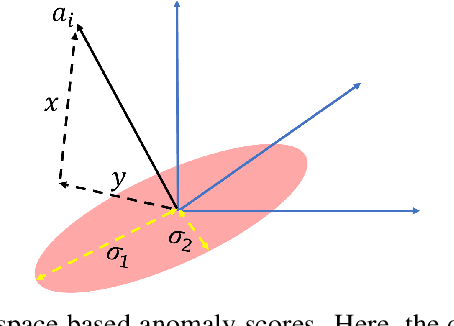
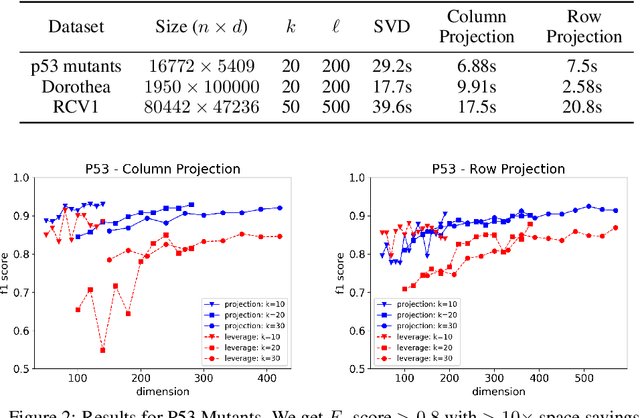
We present efficient streaming algorithms to compute two commonly used anomaly measures: the rank-$k$ leverage scores (aka Mahalanobis distance) and the rank-$k$ projection distance, in the row-streaming model. We show that commonly used matrix sketching techniques such as the Frequent Directions sketch and random projections can be used to approximate these measures. Our main technical contribution is to prove matrix perturbation inequalities for operators arising in the computation of these measures.