KL Divergence Estimation with Multi-group Attribution
Paper and Code
Feb 28, 2022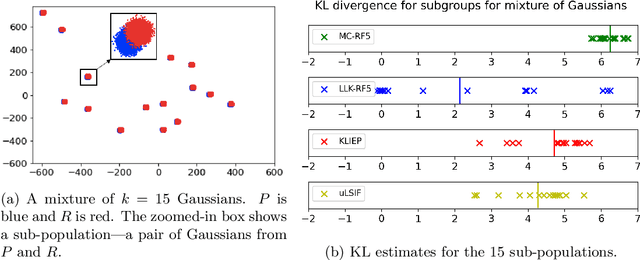



Estimating the Kullback-Leibler (KL) divergence between two distributions given samples from them is well-studied in machine learning and information theory. Motivated by considerations of multi-group fairness, we seek KL divergence estimates that accurately reflect the contributions of sub-populations to the overall divergence. We model the sub-populations coming from a rich (possibly infinite) family $\mathcal{C}$ of overlapping subsets of the domain. We propose the notion of multi-group attribution for $\mathcal{C}$, which requires that the estimated divergence conditioned on every sub-population in $\mathcal{C}$ satisfies some natural accuracy and fairness desiderata, such as ensuring that sub-populations where the model predicts significant divergence do diverge significantly in the two distributions. Our main technical contribution is to show that multi-group attribution can be derived from the recently introduced notion of multi-calibration for importance weights [HKRR18, GRSW21]. We provide experimental evidence to support our theoretical results, and show that multi-group attribution provides better KL divergence estimates when conditioned on sub-populations than other popular algorithms.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge