Faster Anomaly Detection via Matrix Sketching

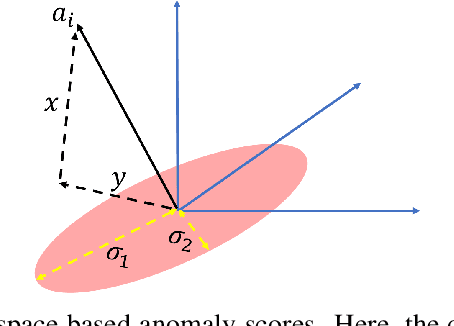
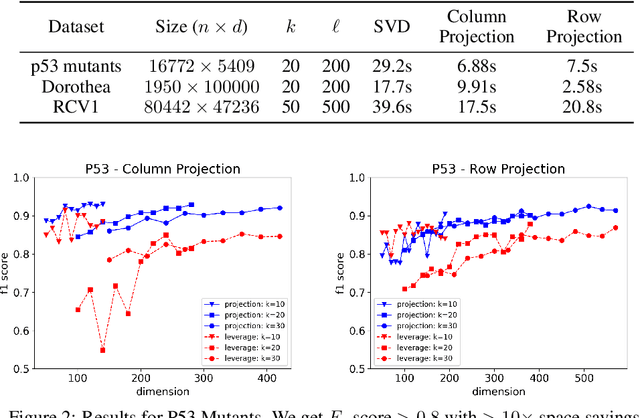
We present efficient streaming algorithms to compute two commonly used anomaly measures: the rank-$k$ leverage scores (aka Mahalanobis distance) and the rank-$k$ projection distance, in the row-streaming model. We show that commonly used matrix sketching techniques such as the Frequent Directions sketch and random projections can be used to approximate these measures. Our main technical contribution is to prove matrix perturbation inequalities for operators arising in the computation of these measures.