Aravind Gollakota
When does a predictor know its own loss?
Feb 27, 2025Abstract:Given a predictor and a loss function, how well can we predict the loss that the predictor will incur on an input? This is the problem of loss prediction, a key computational task associated with uncertainty estimation for a predictor. In a classification setting, a predictor will typically predict a distribution over labels and hence have its own estimate of the loss that it will incur, given by the entropy of the predicted distribution. Should we trust this estimate? In other words, when does the predictor know what it knows and what it does not know? In this work we study the theoretical foundations of loss prediction. Our main contribution is to establish tight connections between nontrivial loss prediction and certain forms of multicalibration, a multigroup fairness notion that asks for calibrated predictions across computationally identifiable subgroups. Formally, we show that a loss predictor that is able to improve on the self-estimate of a predictor yields a witness to a failure of multicalibration, and vice versa. This has the implication that nontrivial loss prediction is in effect no easier or harder than auditing for multicalibration. We support our theoretical results with experiments that show a robust positive correlation between the multicalibration error of a predictor and the efficacy of training a loss predictor.
Provable Uncertainty Decomposition via Higher-Order Calibration
Dec 25, 2024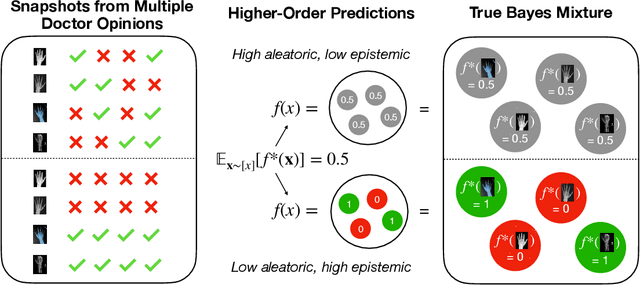
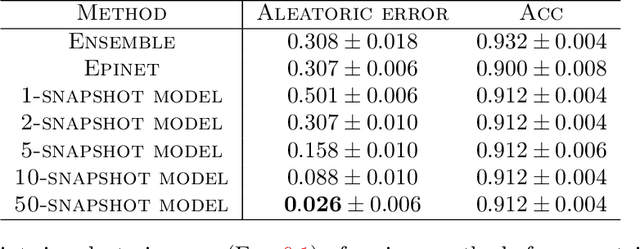
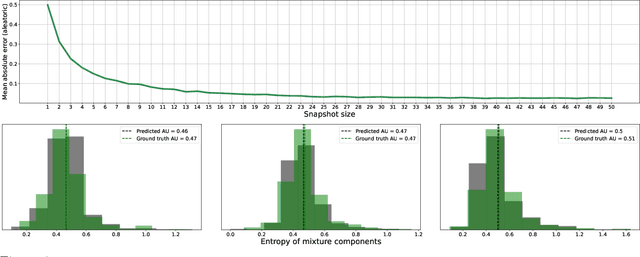
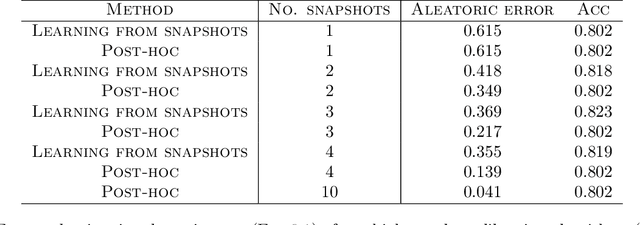
Abstract:We give a principled method for decomposing the predictive uncertainty of a model into aleatoric and epistemic components with explicit semantics relating them to the real-world data distribution. While many works in the literature have proposed such decompositions, they lack the type of formal guarantees we provide. Our method is based on the new notion of higher-order calibration, which generalizes ordinary calibration to the setting of higher-order predictors that predict mixtures over label distributions at every point. We show how to measure as well as achieve higher-order calibration using access to $k$-snapshots, namely examples where each point has $k$ independent conditional labels. Under higher-order calibration, the estimated aleatoric uncertainty at a point is guaranteed to match the real-world aleatoric uncertainty averaged over all points where the prediction is made. To our knowledge, this is the first formal guarantee of this type that places no assumptions whatsoever on the real-world data distribution. Importantly, higher-order calibration is also applicable to existing higher-order predictors such as Bayesian and ensemble models and provides a natural evaluation metric for such models. We demonstrate through experiments that our method produces meaningful uncertainty decompositions for image classification.
Agnostically Learning Single-Index Models using Omnipredictors
Jun 18, 2023Abstract:We give the first result for agnostically learning Single-Index Models (SIMs) with arbitrary monotone and Lipschitz activations. All prior work either held only in the realizable setting or required the activation to be known. Moreover, we only require the marginal to have bounded second moments, whereas all prior work required stronger distributional assumptions (such as anticoncentration or boundedness). Our algorithm is based on recent work by [GHK$^+$23] on omniprediction using predictors satisfying calibrated multiaccuracy. Our analysis is simple and relies on the relationship between Bregman divergences (or matching losses) and $\ell_p$ distances. We also provide new guarantees for standard algorithms like GLMtron and logistic regression in the agnostic setting.
Ambient Diffusion: Learning Clean Distributions from Corrupted Data
May 30, 2023



Abstract:We present the first diffusion-based framework that can learn an unknown distribution using only highly-corrupted samples. This problem arises in scientific applications where access to uncorrupted samples is impossible or expensive to acquire. Another benefit of our approach is the ability to train generative models that are less likely to memorize individual training samples since they never observe clean training data. Our main idea is to introduce additional measurement distortion during the diffusion process and require the model to predict the original corrupted image from the further corrupted image. We prove that our method leads to models that learn the conditional expectation of the full uncorrupted image given this additional measurement corruption. This holds for any corruption process that satisfies some technical conditions (and in particular includes inpainting and compressed sensing). We train models on standard benchmarks (CelebA, CIFAR-10 and AFHQ) and show that we can learn the distribution even when all the training samples have $90\%$ of their pixels missing. We also show that we can finetune foundation models on small corrupted datasets (e.g. MRI scans with block corruptions) and learn the clean distribution without memorizing the training set.
Tester-Learners for Halfspaces: Universal Algorithms
May 19, 2023Abstract:We give the first tester-learner for halfspaces that succeeds universally over a wide class of structured distributions. Our universal tester-learner runs in fully polynomial time and has the following guarantee: the learner achieves error $O(\mathrm{opt}) + \epsilon$ on any labeled distribution that the tester accepts, and moreover, the tester accepts whenever the marginal is any distribution that satisfies a Poincar\'e inequality. In contrast to prior work on testable learning, our tester is not tailored to any single target distribution but rather succeeds for an entire target class of distributions. The class of Poincar\'e distributions includes all strongly log-concave distributions, and, assuming the Kannan--L\'{o}vasz--Simonovits (KLS) conjecture, includes all log-concave distributions. In the special case where the label noise is known to be Massart, our tester-learner achieves error $\mathrm{opt} + \epsilon$ while accepting all log-concave distributions unconditionally (without assuming KLS). Our tests rely on checking hypercontractivity of the unknown distribution using a sum-of-squares (SOS) program, and crucially make use of the fact that Poincar\'e distributions are certifiably hypercontractive in the SOS framework.
An Efficient Tester-Learner for Halfspaces
Mar 13, 2023Abstract:We give the first efficient algorithm for learning halfspaces in the testable learning model recently defined by Rubinfeld and Vasilyan (2023). In this model, a learner certifies that the accuracy of its output hypothesis is near optimal whenever the training set passes an associated test, and training sets drawn from some target distribution -- e.g., the Gaussian -- must pass the test. This model is more challenging than distribution-specific agnostic or Massart noise models where the learner is allowed to fail arbitrarily if the distributional assumption does not hold. We consider the setting where the target distribution is Gaussian (or more generally any strongly log-concave distribution) in $d$ dimensions and the noise model is either Massart or adversarial (agnostic). For Massart noise, our tester-learner runs in polynomial time and outputs a hypothesis with (information-theoretically optimal) error $\mathsf{opt} + \epsilon$ for any strongly log-concave target distribution. For adversarial noise, our tester-learner obtains error $O(\mathsf{opt}) + \epsilon$ in polynomial time when the target distribution is Gaussian; for strongly log-concave distributions, we obtain $\tilde{O}(\mathsf{opt}) + \epsilon$ in quasipolynomial time. Prior work on testable learning ignores the labels in the training set and checks that the empirical moments of the covariates are close to the moments of the base distribution. Here we develop new tests of independent interest that make critical use of the labels and combine them with the moment-matching approach of Gollakota et al. (2023). This enables us to simulate a variant of the algorithm of Diakonikolas et al. (2020) for learning noisy halfspaces using nonconvex SGD but in the testable learning setting.
A Moment-Matching Approach to Testable Learning and a New Characterization of Rademacher Complexity
Nov 23, 2022Abstract:A remarkable recent paper by Rubinfeld and Vasilyan (2022) initiated the study of \emph{testable learning}, where the goal is to replace hard-to-verify distributional assumptions (such as Gaussianity) with efficiently testable ones and to require that the learner succeed whenever the unknown distribution passes the corresponding test. In this model, they gave an efficient algorithm for learning halfspaces under testable assumptions that are provably satisfied by Gaussians. In this paper we give a powerful new approach for developing algorithms for testable learning using tools from moment matching and metric distances in probability. We obtain efficient testable learners for any concept class that admits low-degree \emph{sandwiching polynomials}, capturing most important examples for which we have ordinary agnostic learners. We recover the results of Rubinfeld and Vasilyan as a corollary of our techniques while achieving improved, near-optimal sample complexity bounds for a broad range of concept classes and distributions. Surprisingly, we show that the information-theoretic sample complexity of testable learning is tightly characterized by the Rademacher complexity of the concept class, one of the most well-studied measures in statistical learning theory. In particular, uniform convergence is necessary and sufficient for testable learning. This leads to a fundamental separation from (ordinary) distribution-specific agnostic learning, where uniform convergence is sufficient but not necessary.
Hardness of Noise-Free Learning for Two-Hidden-Layer Neural Networks
Feb 10, 2022
Abstract:We give exponential statistical query (SQ) lower bounds for learning two-hidden-layer ReLU networks with respect to Gaussian inputs in the standard (noise-free) model. No general SQ lower bounds were known for learning ReLU networks of any depth in this setting: previous SQ lower bounds held only for adversarial noise models (agnostic learning) or restricted models such as correlational SQ. Prior work hinted at the impossibility of our result: Vempala and Wilmes showed that general SQ lower bounds cannot apply to any real-valued family of functions that satisfies a simple non-degeneracy condition. To circumvent their result, we refine a lifting procedure due to Daniely and Vardi that reduces Boolean PAC learning problems to Gaussian ones. We show how to extend their technique to other learning models and, in many well-studied cases, obtain a more efficient reduction. As such, we also prove new cryptographic hardness results for PAC learning two-hidden-layer ReLU networks, as well as new lower bounds for learning constant-depth ReLU networks from membership queries.
On the Hardness of PAC-learning stabilizer States with Noise
Feb 09, 2021Abstract:We consider the problem of learning stabilizer states with noise in the Probably Approximately Correct (PAC) framework of Aaronson (2007) for learning quantum states. In the noiseless setting, an algorithm for this problem was recently given by Rocchetto (2018), but the noisy case was left open. Motivated by approaches to noise tolerance from classical learning theory, we introduce the Statistical Query (SQ) model for PAC-learning quantum states, and prove that algorithms in this model are indeed resilient to common forms of noise, including classification and depolarizing noise. We prove an exponential lower bound on learning stabilizer states in the SQ model. Even outside the SQ model, we prove that learning stabilizer states with noise is in general as hard as Learning Parity with Noise (LPN) using classical examples. Our results position the problem of learning stabilizer states as a natural quantum analogue of the classical problem of learning parities: easy in the noiseless setting, but seemingly intractable even with simple forms of noise.
The Polynomial Method is Universal for Distribution-Free Correlational SQ Learning
Oct 29, 2020Abstract:We consider the problem of distribution-free learning for Boolean function classes in the PAC and agnostic models. Generalizing a recent beautiful work of Malach and Shalev-Shwartz (2020) who gave the first tight correlational SQ (CSQ) lower bounds for learning DNF formulas, we show that lower bounds on the threshold or approximate degree of any function class directly imply CSQ lower bounds for PAC or agnostic learning respectively. These match corresponding positive results using upper bounds on the threshold or approximate degree in the SQ model for PAC or agnostic learning. Many of these results were implicit in earlier works of Feldman and Sherstov.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge