Does Generation Require Memorization? Creative Diffusion Models using Ambient Diffusion

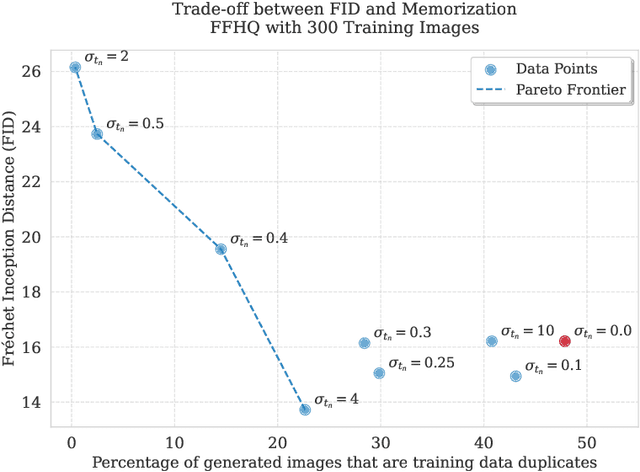
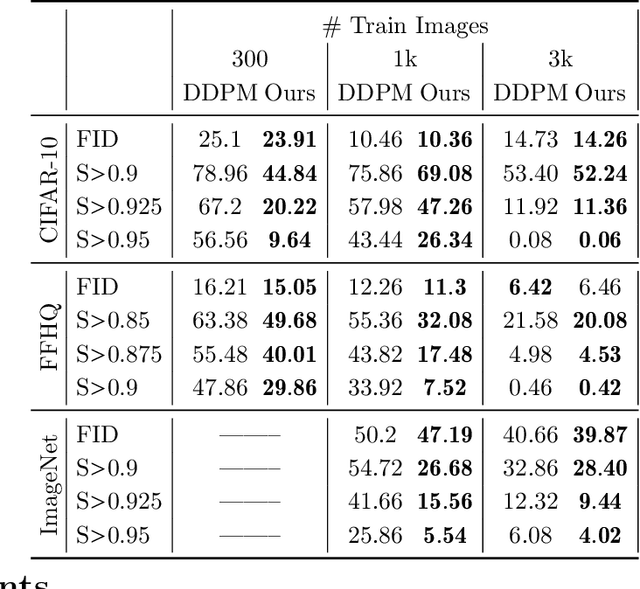
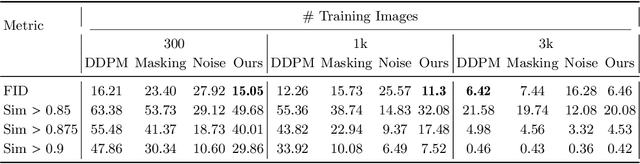
There is strong empirical evidence that the state-of-the-art diffusion modeling paradigm leads to models that memorize the training set, especially when the training set is small. Prior methods to mitigate the memorization problem often lead to a decrease in image quality. Is it possible to obtain strong and creative generative models, i.e., models that achieve high generation quality and low memorization? Despite the current pessimistic landscape of results, we make significant progress in pushing the trade-off between fidelity and memorization. We first provide theoretical evidence that memorization in diffusion models is only necessary for denoising problems at low noise scales (usually used in generating high-frequency details). Using this theoretical insight, we propose a simple, principled method to train the diffusion models using noisy data at large noise scales. We show that our method significantly reduces memorization without decreasing the image quality, for both text-conditional and unconditional models and for a variety of data availability settings.

Learning Neural Networks with Distribution Shift: Efficiently Certifiable Guarantees

We give the first provably efficient algorithms for learning neural networks with distribution shift. We work in the Testable Learning with Distribution Shift framework (TDS learning) of Klivans et al. (2024), where the learner receives labeled examples from a training distribution and unlabeled examples from a test distribution and must either output a hypothesis with low test error or reject if distribution shift is detected. No assumptions are made on the test distribution. All prior work in TDS learning focuses on classification, while here we must handle the setting of nonconvex regression. Our results apply to real-valued networks with arbitrary Lipschitz activations and work whenever the training distribution has strictly sub-exponential tails. For training distributions that are bounded and hypercontractive, we give a fully polynomial-time algorithm for TDS learning one hidden-layer networks with sigmoid activations. We achieve this by importing classical kernel methods into the TDS framework using data-dependent feature maps and a type of kernel matrix that couples samples from both train and test distributions.

Testing Noise Assumptions of Learning Algorithms

We pose a fundamental question in computational learning theory: can we efficiently test whether a training set satisfies the assumptions of a given noise model? This question has remained unaddressed despite decades of research on learning in the presence of noise. In this work, we show that this task is tractable and present the first efficient algorithm to test various noise assumptions on the training data. To model this question, we extend the recently proposed testable learning framework of Rubinfeld and Vasilyan (2023) and require a learner to run an associated test that satisfies the following two conditions: (1) whenever the test accepts, the learner outputs a classifier along with a certificate of optimality, and (2) the test must pass for any dataset drawn according to a specified modeling assumption on both the marginal distribution and the noise model. We then consider the problem of learning halfspaces over Gaussian marginals with Massart noise (where each label can be flipped with probability less than $1/2$ depending on the input features), and give a fully-polynomial time testable learning algorithm. We also show a separation between the classical setting of learning in the presence of structured noise and testable learning. In fact, for the simple case of random classification noise (where each label is flipped with fixed probability $\eta = 1/2$), we show that testable learning requires super-polynomial time while classical learning is trivial.

Learning Constant-Depth Circuits in Malicious Noise Models

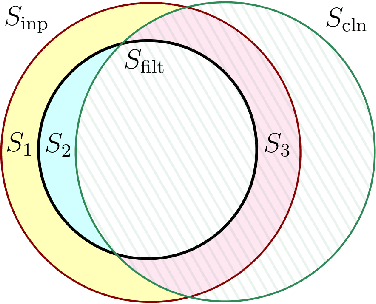
The seminal work of Linial, Mansour, and Nisan gave a quasipolynomial-time algorithm for learning constant-depth circuits ($\mathsf{AC}^0$) with respect to the uniform distribution on the hypercube. Extending their algorithm to the setting of malicious noise, where both covariates and labels can be adversarially corrupted, has remained open. Here we achieve such a result, inspired by recent work on learning with distribution shift. Our running time essentially matches their algorithm, which is known to be optimal assuming various cryptographic primitives. Our proof uses a simple outlier-removal method combined with Braverman's theorem for fooling constant-depth circuits. We attain the best possible dependence on the noise rate and succeed in the harshest possible noise model (i.e., contamination or so-called "nasty noise").

Efficient Discrepancy Testing for Learning with Distribution Shift

A fundamental notion of distance between train and test distributions from the field of domain adaptation is discrepancy distance. While in general hard to compute, here we provide the first set of provably efficient algorithms for testing localized discrepancy distance, where discrepancy is computed with respect to a fixed output classifier. These results imply a broad set of new, efficient learning algorithms in the recently introduced model of Testable Learning with Distribution Shift (TDS learning) due to Klivans et al. (2023). Our approach generalizes and improves all prior work on TDS learning: (1) we obtain universal learners that succeed simultaneously for large classes of test distributions, (2) achieve near-optimal error rates, and (3) give exponential improvements for constant depth circuits. Our methods further extend to semi-parametric settings and imply the first positive results for low-dimensional convex sets. Additionally, we separate learning and testing phases and obtain algorithms that run in fully polynomial time at test time.

Learning Intersections of Halfspaces with Distribution Shift: Improved Algorithms and SQ Lower Bounds

Recent work of Klivans, Stavropoulos, and Vasilyan initiated the study of testable learning with distribution shift (TDS learning), where a learner is given labeled samples from training distribution $\mathcal{D}$, unlabeled samples from test distribution $\mathcal{D}'$, and the goal is to output a classifier with low error on $\mathcal{D}'$ whenever the training samples pass a corresponding test. Their model deviates from all prior work in that no assumptions are made on $\mathcal{D}'$. Instead, the test must accept (with high probability) when the marginals of the training and test distributions are equal. Here we focus on the fundamental case of intersections of halfspaces with respect to Gaussian training distributions and prove a variety of new upper bounds including a $2^{(k/\epsilon)^{O(1)}} \mathsf{poly}(d)$-time algorithm for TDS learning intersections of $k$ homogeneous halfspaces to accuracy $\epsilon$ (prior work achieved $d^{(k/\epsilon)^{O(1)}}$). We work under the mild assumption that the Gaussian training distribution contains at least an $\epsilon$ fraction of both positive and negative examples ($\epsilon$-balanced). We also prove the first set of SQ lower-bounds for any TDS learning problem and show (1) the $\epsilon$-balanced assumption is necessary for $\mathsf{poly}(d,1/\epsilon)$-time TDS learning for a single halfspace and (2) a $d^{\tilde{\Omega}(\log 1/\epsilon)}$ lower bound for the intersection of two general halfspaces, even with the $\epsilon$-balanced assumption. Our techniques significantly expand the toolkit for TDS learning. We use dimension reduction and coverings to give efficient algorithms for computing a localized version of discrepancy distance, a key metric from the domain adaptation literature.

Testable Learning with Distribution Shift

We revisit the fundamental problem of learning with distribution shift, in which a learner is given labeled samples from training distribution $D$, unlabeled samples from test distribution $D'$ and is asked to output a classifier with low test error. The standard approach in this setting is to bound the loss of a classifier in terms of some notion of distance between $D$ and $D'$. These distances, however, seem difficult to compute and do not lead to efficient algorithms. We depart from this paradigm and define a new model called testable learning with distribution shift, where we can obtain provably efficient algorithms for certifying the performance of a classifier on a test distribution. In this model, a learner outputs a classifier with low test error whenever samples from $D$ and $D'$ pass an associated test; moreover, the test must accept if the marginal of $D$ equals the marginal of $D'$. We give several positive results for learning well-studied concept classes such as halfspaces, intersections of halfspaces, and decision trees when the marginal of $D$ is Gaussian or uniform on $\{\pm 1\}^d$. Prior to our work, no efficient algorithms for these basic cases were known without strong assumptions on $D'$. For halfspaces in the realizable case (where there exists a halfspace consistent with both $D$ and $D'$), we combine a moment-matching approach with ideas from active learning to simulate an efficient oracle for estimating disagreement regions. To extend to the non-realizable setting, we apply recent work from testable (agnostic) learning. More generally, we prove that any function class with low-degree $L_2$-sandwiching polynomial approximators can be learned in our model. We apply constructions from the pseudorandomness literature to obtain the required approximators.

Agnostically Learning Single-Index Models using Omnipredictors

We give the first result for agnostically learning Single-Index Models (SIMs) with arbitrary monotone and Lipschitz activations. All prior work either held only in the realizable setting or required the activation to be known. Moreover, we only require the marginal to have bounded second moments, whereas all prior work required stronger distributional assumptions (such as anticoncentration or boundedness). Our algorithm is based on recent work by [GHK$^+$23] on omniprediction using predictors satisfying calibrated multiaccuracy. Our analysis is simple and relies on the relationship between Bregman divergences (or matching losses) and $\ell_p$ distances. We also provide new guarantees for standard algorithms like GLMtron and logistic regression in the agnostic setting.

Tester-Learners for Halfspaces: Universal Algorithms

We give the first tester-learner for halfspaces that succeeds universally over a wide class of structured distributions. Our universal tester-learner runs in fully polynomial time and has the following guarantee: the learner achieves error $O(\mathrm{opt}) + \epsilon$ on any labeled distribution that the tester accepts, and moreover, the tester accepts whenever the marginal is any distribution that satisfies a Poincar\'e inequality. In contrast to prior work on testable learning, our tester is not tailored to any single target distribution but rather succeeds for an entire target class of distributions. The class of Poincar\'e distributions includes all strongly log-concave distributions, and, assuming the Kannan--L\'{o}vasz--Simonovits (KLS) conjecture, includes all log-concave distributions. In the special case where the label noise is known to be Massart, our tester-learner achieves error $\mathrm{opt} + \epsilon$ while accepting all log-concave distributions unconditionally (without assuming KLS). Our tests rely on checking hypercontractivity of the unknown distribution using a sum-of-squares (SOS) program, and crucially make use of the fact that Poincar\'e distributions are certifiably hypercontractive in the SOS framework.

An Efficient Tester-Learner for Halfspaces

We give the first efficient algorithm for learning halfspaces in the testable learning model recently defined by Rubinfeld and Vasilyan (2023). In this model, a learner certifies that the accuracy of its output hypothesis is near optimal whenever the training set passes an associated test, and training sets drawn from some target distribution -- e.g., the Gaussian -- must pass the test. This model is more challenging than distribution-specific agnostic or Massart noise models where the learner is allowed to fail arbitrarily if the distributional assumption does not hold. We consider the setting where the target distribution is Gaussian (or more generally any strongly log-concave distribution) in $d$ dimensions and the noise model is either Massart or adversarial (agnostic). For Massart noise, our tester-learner runs in polynomial time and outputs a hypothesis with (information-theoretically optimal) error $\mathsf{opt} + \epsilon$ for any strongly log-concave target distribution. For adversarial noise, our tester-learner obtains error $O(\mathsf{opt}) + \epsilon$ in polynomial time when the target distribution is Gaussian; for strongly log-concave distributions, we obtain $\tilde{O}(\mathsf{opt}) + \epsilon$ in quasipolynomial time. Prior work on testable learning ignores the labels in the training set and checks that the empirical moments of the covariates are close to the moments of the base distribution. Here we develop new tests of independent interest that make critical use of the labels and combine them with the moment-matching approach of Gollakota et al. (2023). This enables us to simulate a variant of the algorithm of Diakonikolas et al. (2020) for learning noisy halfspaces using nonconvex SGD but in the testable learning setting.