A Fully Polynomial-Time Algorithm for Robustly Learning Halfspaces over the Hypercube

We give the first fully polynomial-time algorithm for learning halfspaces with respect to the uniform distribution on the hypercube in the presence of contamination, where an adversary may corrupt some fraction of examples and labels arbitrarily. We achieve an error guarantee of $η^{O(1)}+ε$ where $η$ is the noise rate. Such a result was not known even in the agnostic setting, where only labels can be adversarially corrupted. All prior work over the last two decades has a superpolynomial dependence in $1/ε$ or succeeds only with respect to continuous marginals (such as log-concave densities). Previous analyses rely heavily on various structural properties of continuous distributions such as anti-concentration. Our approach avoids these requirements and makes use of a new algorithm for learning Generalized Linear Models (GLMs) with only a polylogarithmic dependence on the activation function's Lipschitz constant. More generally, our framework shows that supervised learning with respect to discrete distributions is not as difficult as previously thought.

Sparse Linear Regression is Easy on Random Supports

Sparse linear regression is one of the most basic questions in machine learning and statistics. Here, we are given as input a design matrix $X \in \mathbb{R}^{N \times d}$ and measurements or labels ${y} \in \mathbb{R}^N$ where ${y} = {X} {w}^* + ξ$, and $ξ$ is the noise in the measurements. Importantly, we have the additional constraint that the unknown signal vector ${w}^*$ is sparse: it has $k$ non-zero entries where $k$ is much smaller than the ambient dimension. Our goal is to output a prediction vector $\widehat{w}$ that has small prediction error: $\frac{1}{N}\cdot \|{X} {w}^* - {X} \widehat{w}\|^2_2$. Information-theoretically, we know what is best possible in terms of measurements: under most natural noise distributions, we can get prediction error at most $ε$ with roughly $N = O(k \log d/ε)$ samples. Computationally, this currently needs $d^{Ω(k)}$ run-time. Alternately, with $N = O(d)$, we can get polynomial-time. Thus, there is an exponential gap (in the dependence on $d$) between the two and we do not know if it is possible to get $d^{o(k)}$ run-time and $o(d)$ samples. We give the first generic positive result for worst-case design matrices ${X}$: For any ${X}$, we show that if the support of ${w}^*$ is chosen at random, we can get prediction error $ε$ with $N = \text{poly}(k, \log d, 1/ε)$ samples and run-time $\text{poly}(d,N)$. This run-time holds for any design matrix ${X}$ with condition number up to $2^{\text{poly}(d)}$. Previously, such results were known for worst-case ${w}^*$, but only for random design matrices from well-behaved families, matrices that have a very low condition number ($\text{poly}(\log d)$; e.g., as studied in compressed sensing), or those with special structural properties.

Learning Neural Networks with Distribution Shift: Efficiently Certifiable Guarantees

We give the first provably efficient algorithms for learning neural networks with distribution shift. We work in the Testable Learning with Distribution Shift framework (TDS learning) of Klivans et al. (2024), where the learner receives labeled examples from a training distribution and unlabeled examples from a test distribution and must either output a hypothesis with low test error or reject if distribution shift is detected. No assumptions are made on the test distribution. All prior work in TDS learning focuses on classification, while here we must handle the setting of nonconvex regression. Our results apply to real-valued networks with arbitrary Lipschitz activations and work whenever the training distribution has strictly sub-exponential tails. For training distributions that are bounded and hypercontractive, we give a fully polynomial-time algorithm for TDS learning one hidden-layer networks with sigmoid activations. We achieve this by importing classical kernel methods into the TDS framework using data-dependent feature maps and a type of kernel matrix that couples samples from both train and test distributions.

Learning the Sherrington-Kirkpatrick Model Even at Low Temperature

We consider the fundamental problem of learning the parameters of an undirected graphical model or Markov Random Field (MRF) in the setting where the edge weights are chosen at random. For Ising models, we show that a multiplicative-weight update algorithm due to Klivans and Meka learns the parameters in polynomial time for any inverse temperature $\beta \leq \sqrt{\log n}$. This immediately yields an algorithm for learning the Sherrington-Kirkpatrick (SK) model beyond the high-temperature regime of $\beta < 1$. Prior work breaks down at $\beta = 1$ and requires heavy machinery from statistical physics or functional inequalities. In contrast, our analysis is relatively simple and uses only subgaussian concentration. Our results extend to MRFs of higher order (such as pure $p$-spin models), where even results in the high-temperature regime were not known.

Smoothed Analysis for Learning Concepts with Low Intrinsic Dimension

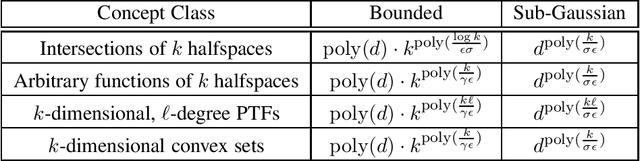
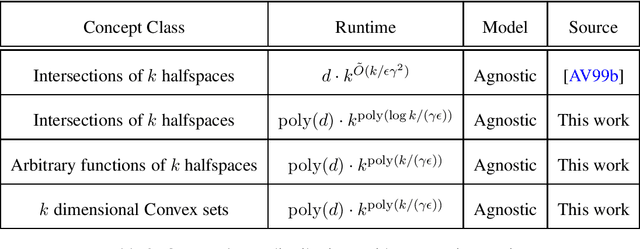
In traditional models of supervised learning, the goal of a learner -- given examples from an arbitrary joint distribution on $\mathbb{R}^d \times \{\pm 1\}$ -- is to output a hypothesis that is competitive (to within $\epsilon$) of the best fitting concept from some class. In order to escape strong hardness results for learning even simple concept classes, we introduce a smoothed-analysis framework that requires a learner to compete only with the best classifier that is robust to small random Gaussian perturbation. This subtle change allows us to give a wide array of learning results for any concept that (1) depends on a low-dimensional subspace (aka multi-index model) and (2) has a bounded Gaussian surface area. This class includes functions of halfspaces and (low-dimensional) convex sets, cases that are only known to be learnable in non-smoothed settings with respect to highly structured distributions such as Gaussians. Surprisingly, our analysis also yields new results for traditional non-smoothed frameworks such as learning with margin. In particular, we obtain the first algorithm for agnostically learning intersections of $k$-halfspaces in time $k^{poly(\frac{\log k}{\epsilon \gamma}) }$ where $\gamma$ is the margin parameter. Before our work, the best-known runtime was exponential in $k$ (Arriaga and Vempala, 1999).

Efficient Discrepancy Testing for Learning with Distribution Shift

A fundamental notion of distance between train and test distributions from the field of domain adaptation is discrepancy distance. While in general hard to compute, here we provide the first set of provably efficient algorithms for testing localized discrepancy distance, where discrepancy is computed with respect to a fixed output classifier. These results imply a broad set of new, efficient learning algorithms in the recently introduced model of Testable Learning with Distribution Shift (TDS learning) due to Klivans et al. (2023). Our approach generalizes and improves all prior work on TDS learning: (1) we obtain universal learners that succeed simultaneously for large classes of test distributions, (2) achieve near-optimal error rates, and (3) give exponential improvements for constant depth circuits. Our methods further extend to semi-parametric settings and imply the first positive results for low-dimensional convex sets. Additionally, we separate learning and testing phases and obtain algorithms that run in fully polynomial time at test time.

Online Learning in Adversarial MDPs: Is the Communicating Case Harder than Ergodic?

We study online learning in adversarial communicating Markov Decision Processes with full information. We give an algorithm that achieves a regret of $O(\sqrt{T})$ with respect to the best fixed deterministic policy in hindsight when the transitions are deterministic. We also prove a regret lower bound in this setting which is tight up to polynomial factors in the MDP parameters. We also give an inefficient algorithm that achieves $O(\sqrt{T})$ regret in communicating MDPs (with an additional mild restriction on the transition dynamics).