The Power of Iterative Filtering for Supervised Learning with (Heavy) Contamination

Inspired by recent work on learning with distribution shift, we give a general outlier removal algorithm called iterative polynomial filtering and show a number of striking applications for supervised learning with contamination: (1) We show that any function class that can be approximated by low-degree polynomials with respect to a hypercontractive distribution can be efficiently learned under bounded contamination (also known as nasty noise). This is a surprising resolution to a longstanding gap between the complexity of agnostic learning and learning with contamination, as it was widely believed that low-degree approximators only implied tolerance to label noise. (2) For any function class that admits the (stronger) notion of sandwiching approximators, we obtain near-optimal learning guarantees even with respect to heavy additive contamination, where far more than $1/2$ of the training set may be added adversarially. Prior related work held only for regression and in a list-decodable setting. (3) We obtain the first efficient algorithms for tolerant testable learning of functions of halfspaces with respect to any fixed log-concave distribution. Even the non-tolerant case for a single halfspace in this setting had remained open. These results significantly advance our understanding of efficient supervised learning under contamination, a setting that has been much less studied than its unsupervised counterpart.

Robust learning of halfspaces under log-concave marginals

We say that a classifier is \emph{adversarially robust} to perturbations of norm $r$ if, with high probability over a point $x$ drawn from the input distribution, there is no point within distance $\le r$ from $x$ that is classified differently. The \emph{boundary volume} is the probability that a point falls within distance $r$ of a point with a different label. This work studies the task of computationally efficient learning of hypotheses with small boundary volume, where the input is distributed as a subgaussian isotropic log-concave distribution over $\mathbb{R}^d$. Linear threshold functions are adversarially robust; they have boundary volume proportional to $r$. Such concept classes are efficiently learnable by polynomial regression, which produces a polynomial threshold function (PTF), but PTFs in general may have boundary volume $\Omega(1)$, even for $r \ll 1$. We give an algorithm that agnostically learns linear threshold functions and returns a classifier with boundary volume $O(r+\varepsilon)$ at radius of perturbation $r$. The time and sample complexity of $d^{\tilde{O}(1/\varepsilon^2)}$ matches the complexity of polynomial regression. Our algorithm augments the classic approach of polynomial regression with three additional steps: a) performing the $\ell_1$-error regression under noise sensitivity constraints, b) a structured partitioning and rounding step that returns a Boolean classifier with error $\textsf{opt} + O(\varepsilon)$ and noise sensitivity $O(r+\varepsilon)$ simultaneously, and c) a local corrector that ``smooths'' a function with low noise sensitivity into a function that is adversarially robust.

Testing Noise Assumptions of Learning Algorithms

We pose a fundamental question in computational learning theory: can we efficiently test whether a training set satisfies the assumptions of a given noise model? This question has remained unaddressed despite decades of research on learning in the presence of noise. In this work, we show that this task is tractable and present the first efficient algorithm to test various noise assumptions on the training data. To model this question, we extend the recently proposed testable learning framework of Rubinfeld and Vasilyan (2023) and require a learner to run an associated test that satisfies the following two conditions: (1) whenever the test accepts, the learner outputs a classifier along with a certificate of optimality, and (2) the test must pass for any dataset drawn according to a specified modeling assumption on both the marginal distribution and the noise model. We then consider the problem of learning halfspaces over Gaussian marginals with Massart noise (where each label can be flipped with probability less than $1/2$ depending on the input features), and give a fully-polynomial time testable learning algorithm. We also show a separation between the classical setting of learning in the presence of structured noise and testable learning. In fact, for the simple case of random classification noise (where each label is flipped with fixed probability $\eta = 1/2$), we show that testable learning requires super-polynomial time while classical learning is trivial.

Learning Constant-Depth Circuits in Malicious Noise Models

The seminal work of Linial, Mansour, and Nisan gave a quasipolynomial-time algorithm for learning constant-depth circuits ($\mathsf{AC}^0$) with respect to the uniform distribution on the hypercube. Extending their algorithm to the setting of malicious noise, where both covariates and labels can be adversarially corrupted, has remained open. Here we achieve such a result, inspired by recent work on learning with distribution shift. Our running time essentially matches their algorithm, which is known to be optimal assuming various cryptographic primitives. Our proof uses a simple outlier-removal method combined with Braverman's theorem for fooling constant-depth circuits. We attain the best possible dependence on the noise rate and succeed in the harshest possible noise model (i.e., contamination or so-called "nasty noise").

Efficient Discrepancy Testing for Learning with Distribution Shift

A fundamental notion of distance between train and test distributions from the field of domain adaptation is discrepancy distance. While in general hard to compute, here we provide the first set of provably efficient algorithms for testing localized discrepancy distance, where discrepancy is computed with respect to a fixed output classifier. These results imply a broad set of new, efficient learning algorithms in the recently introduced model of Testable Learning with Distribution Shift (TDS learning) due to Klivans et al. (2023). Our approach generalizes and improves all prior work on TDS learning: (1) we obtain universal learners that succeed simultaneously for large classes of test distributions, (2) achieve near-optimal error rates, and (3) give exponential improvements for constant depth circuits. Our methods further extend to semi-parametric settings and imply the first positive results for low-dimensional convex sets. Additionally, we separate learning and testing phases and obtain algorithms that run in fully polynomial time at test time.

Tolerant Algorithms for Learning with Arbitrary Covariate Shift

We study the problem of learning under arbitrary distribution shift, where the learner is trained on a labeled set from one distribution but evaluated on a different, potentially adversarially generated test distribution. We focus on two frameworks: PQ learning [Goldwasser, A. Kalai, Y. Kalai, Montasser NeurIPS 2020], allowing abstention on adversarially generated parts of the test distribution, and TDS learning [Klivans, Stavropoulos, Vasilyan COLT 2024], permitting abstention on the entire test distribution if distribution shift is detected. All prior known algorithms either rely on learning primitives that are computationally hard even for simple function classes, or end up abstaining entirely even in the presence of a tiny amount of distribution shift. We address both these challenges for natural function classes, including intersections of halfspaces and decision trees, and standard training distributions, including Gaussians. For PQ learning, we give efficient learning algorithms, while for TDS learning, our algorithms can tolerate moderate amounts of distribution shift. At the core of our approach is an improved analysis of spectral outlier-removal techniques from learning with nasty noise. Our analysis can (1) handle arbitrarily large fraction of outliers, which is crucial for handling arbitrary distribution shifts, and (2) obtain stronger bounds on polynomial moments of the distribution after outlier removal, yielding new insights into polynomial regression under distribution shifts. Lastly, our techniques lead to novel results for tolerant testable learning [Rubinfeld and Vasilyan STOC 2023], and learning with nasty noise.

Learning Intersections of Halfspaces with Distribution Shift: Improved Algorithms and SQ Lower Bounds

Recent work of Klivans, Stavropoulos, and Vasilyan initiated the study of testable learning with distribution shift (TDS learning), where a learner is given labeled samples from training distribution $\mathcal{D}$, unlabeled samples from test distribution $\mathcal{D}'$, and the goal is to output a classifier with low error on $\mathcal{D}'$ whenever the training samples pass a corresponding test. Their model deviates from all prior work in that no assumptions are made on $\mathcal{D}'$. Instead, the test must accept (with high probability) when the marginals of the training and test distributions are equal. Here we focus on the fundamental case of intersections of halfspaces with respect to Gaussian training distributions and prove a variety of new upper bounds including a $2^{(k/\epsilon)^{O(1)}} \mathsf{poly}(d)$-time algorithm for TDS learning intersections of $k$ homogeneous halfspaces to accuracy $\epsilon$ (prior work achieved $d^{(k/\epsilon)^{O(1)}}$). We work under the mild assumption that the Gaussian training distribution contains at least an $\epsilon$ fraction of both positive and negative examples ($\epsilon$-balanced). We also prove the first set of SQ lower-bounds for any TDS learning problem and show (1) the $\epsilon$-balanced assumption is necessary for $\mathsf{poly}(d,1/\epsilon)$-time TDS learning for a single halfspace and (2) a $d^{\tilde{\Omega}(\log 1/\epsilon)}$ lower bound for the intersection of two general halfspaces, even with the $\epsilon$-balanced assumption. Our techniques significantly expand the toolkit for TDS learning. We use dimension reduction and coverings to give efficient algorithms for computing a localized version of discrepancy distance, a key metric from the domain adaptation literature.

Testable Learning with Distribution Shift

We revisit the fundamental problem of learning with distribution shift, in which a learner is given labeled samples from training distribution $D$, unlabeled samples from test distribution $D'$ and is asked to output a classifier with low test error. The standard approach in this setting is to bound the loss of a classifier in terms of some notion of distance between $D$ and $D'$. These distances, however, seem difficult to compute and do not lead to efficient algorithms. We depart from this paradigm and define a new model called testable learning with distribution shift, where we can obtain provably efficient algorithms for certifying the performance of a classifier on a test distribution. In this model, a learner outputs a classifier with low test error whenever samples from $D$ and $D'$ pass an associated test; moreover, the test must accept if the marginal of $D$ equals the marginal of $D'$. We give several positive results for learning well-studied concept classes such as halfspaces, intersections of halfspaces, and decision trees when the marginal of $D$ is Gaussian or uniform on $\{\pm 1\}^d$. Prior to our work, no efficient algorithms for these basic cases were known without strong assumptions on $D'$. For halfspaces in the realizable case (where there exists a halfspace consistent with both $D$ and $D'$), we combine a moment-matching approach with ideas from active learning to simulate an efficient oracle for estimating disagreement regions. To extend to the non-realizable setting, we apply recent work from testable (agnostic) learning. More generally, we prove that any function class with low-degree $L_2$-sandwiching polynomial approximators can be learned in our model. We apply constructions from the pseudorandomness literature to obtain the required approximators.

Tester-Learners for Halfspaces: Universal Algorithms

We give the first tester-learner for halfspaces that succeeds universally over a wide class of structured distributions. Our universal tester-learner runs in fully polynomial time and has the following guarantee: the learner achieves error $O(\mathrm{opt}) + \epsilon$ on any labeled distribution that the tester accepts, and moreover, the tester accepts whenever the marginal is any distribution that satisfies a Poincar\'e inequality. In contrast to prior work on testable learning, our tester is not tailored to any single target distribution but rather succeeds for an entire target class of distributions. The class of Poincar\'e distributions includes all strongly log-concave distributions, and, assuming the Kannan--L\'{o}vasz--Simonovits (KLS) conjecture, includes all log-concave distributions. In the special case where the label noise is known to be Massart, our tester-learner achieves error $\mathrm{opt} + \epsilon$ while accepting all log-concave distributions unconditionally (without assuming KLS). Our tests rely on checking hypercontractivity of the unknown distribution using a sum-of-squares (SOS) program, and crucially make use of the fact that Poincar\'e distributions are certifiably hypercontractive in the SOS framework.

Agnostic proper learning of monotone functions: beyond the black-box correction barrier

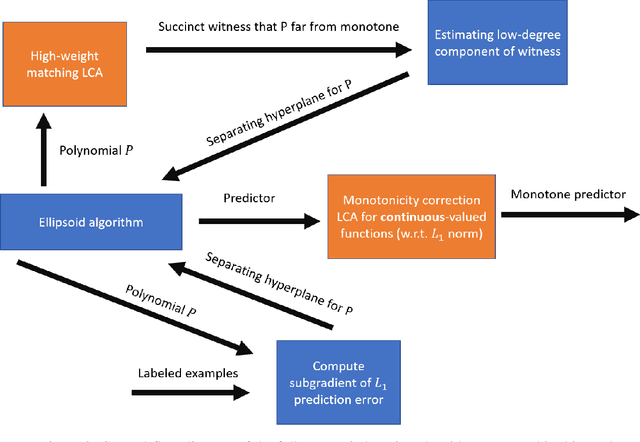
We give the first agnostic, efficient, proper learning algorithm for monotone Boolean functions. Given $2^{\tilde{O}(\sqrt{n}/\varepsilon)}$ uniformly random examples of an unknown function $f:\{\pm 1\}^n \rightarrow \{\pm 1\}$, our algorithm outputs a hypothesis $g:\{\pm 1\}^n \rightarrow \{\pm 1\}$ that is monotone and $(\mathrm{opt} + \varepsilon)$-close to $f$, where $\mathrm{opt}$ is the distance from $f$ to the closest monotone function. The running time of the algorithm (and consequently the size and evaluation time of the hypothesis) is also $2^{\tilde{O}(\sqrt{n}/\varepsilon)}$, nearly matching the lower bound of Blais et al (RANDOM '15). We also give an algorithm for estimating up to additive error $\varepsilon$ the distance of an unknown function $f$ to monotone using a run-time of $2^{\tilde{O}(\sqrt{n}/\varepsilon)}$. Previously, for both of these problems, sample-efficient algorithms were known, but these algorithms were not run-time efficient. Our work thus closes this gap in our knowledge between the run-time and sample complexity. This work builds upon the improper learning algorithm of Bshouty and Tamon (JACM '96) and the proper semiagnostic learning algorithm of Lange, Rubinfeld, and Vasilyan (FOCS '22), which obtains a non-monotone Boolean-valued hypothesis, then ``corrects'' it to monotone using query-efficient local computation algorithms on graphs. This black-box correction approach can achieve no error better than $2\mathrm{opt} + \varepsilon$ information-theoretically; we bypass this barrier by a) augmenting the improper learner with a convex optimization step, and b) learning and correcting a real-valued function before rounding its values to Boolean. Our real-valued correction algorithm solves the ``poset sorting'' problem of [LRV22] for functions over general posets with non-Boolean labels.