Mihir Singhal
Omnipredictors for Regression and the Approximate Rank of Convex Functions
Jan 26, 2024Abstract:Consider the supervised learning setting where the goal is to learn to predict labels $\mathbf y$ given points $\mathbf x$ from a distribution. An \textit{omnipredictor} for a class $\mathcal L$ of loss functions and a class $\mathcal C$ of hypotheses is a predictor whose predictions incur less expected loss than the best hypothesis in $\mathcal C$ for every loss in $\mathcal L$. Since the work of [GKR+21] that introduced the notion, there has been a large body of work in the setting of binary labels where $\mathbf y \in \{0, 1\}$, but much less is known about the regression setting where $\mathbf y \in [0,1]$ can be continuous. Our main conceptual contribution is the notion of \textit{sufficient statistics} for loss minimization over a family of loss functions: these are a set of statistics about a distribution such that knowing them allows one to take actions that minimize the expected loss for any loss in the family. The notion of sufficient statistics relates directly to the approximate rank of the family of loss functions. Our key technical contribution is a bound of $O(1/\varepsilon^{2/3})$ on the $\epsilon$-approximate rank of convex, Lipschitz functions on the interval $[0,1]$, which we show is tight up to a factor of $\mathrm{polylog} (1/\epsilon)$. This yields improved runtimes for learning omnipredictors for the class of all convex, Lipschitz loss functions under weak learnability assumptions about the class $\mathcal C$. We also give efficient omnipredictors when the loss families have low-degree polynomial approximations, or arise from generalized linear models (GLMs). This translation from sufficient statistics to faster omnipredictors is made possible by lifting the technique of loss outcome indistinguishability introduced by [GKH+23] for Boolean labels to the regression setting.
Low-Degree Multicalibration
Mar 02, 2022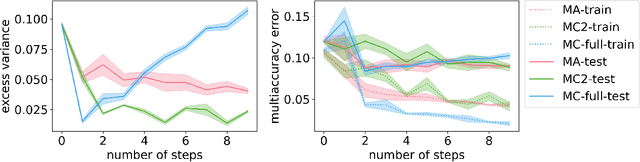
Abstract:Introduced as a notion of algorithmic fairness, multicalibration has proved to be a powerful and versatile concept with implications far beyond its original intent. This stringent notion -- that predictions be well-calibrated across a rich class of intersecting subpopulations -- provides its strong guarantees at a cost: the computational and sample complexity of learning multicalibrated predictors are high, and grow exponentially with the number of class labels. In contrast, the relaxed notion of multiaccuracy can be achieved more efficiently, yet many of the most desirable properties of multicalibration cannot be guaranteed assuming multiaccuracy alone. This tension raises a key question: Can we learn predictors with multicalibration-style guarantees at a cost commensurate with multiaccuracy? In this work, we define and initiate the study of Low-Degree Multicalibration. Low-Degree Multicalibration defines a hierarchy of increasingly-powerful multi-group fairness notions that spans multiaccuracy and the original formulation of multicalibration at the extremes. Our main technical contribution demonstrates that key properties of multicalibration, related to fairness and accuracy, actually manifest as low-degree properties. Importantly, we show that low-degree multicalibration can be significantly more efficient than full multicalibration. In the multi-class setting, the sample complexity to achieve low-degree multicalibration improves exponentially (in the number of classes) over full multicalibration. Our work presents compelling evidence that low-degree multicalibration represents a sweet spot, pairing computational and sample efficiency with strong fairness and accuracy guarantees.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge