Multi-Task Learning for Sparsity Pattern Heterogeneity: A Discrete Optimization Approach

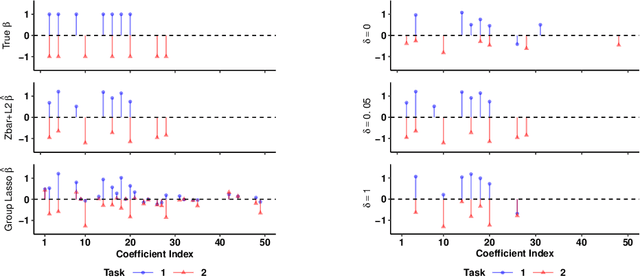
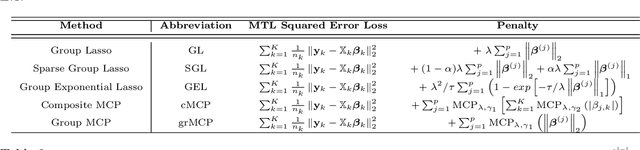
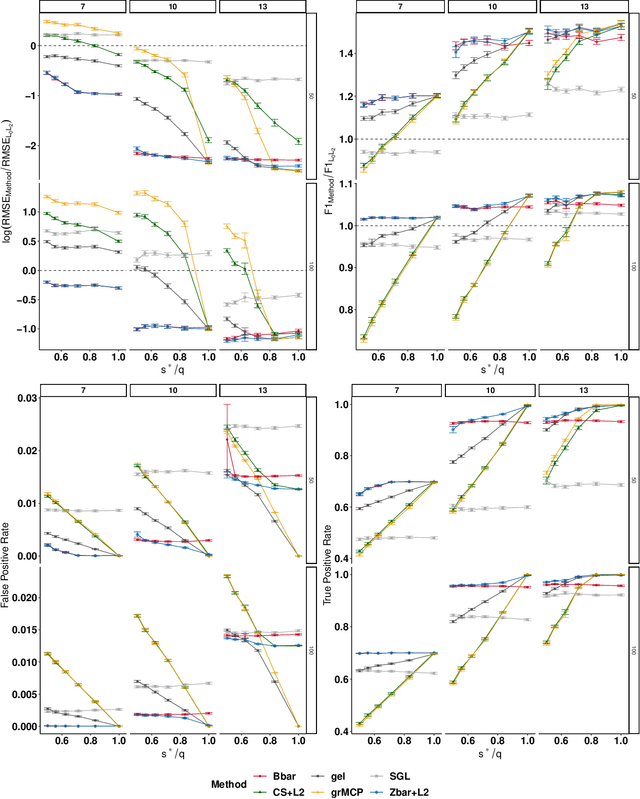
We extend best-subset selection to linear Multi-Task Learning (MTL), where a set of linear models are jointly trained on a collection of datasets (``tasks''). Allowing the regression coefficients of tasks to have different sparsity patterns (i.e., different supports), we propose a modeling framework for MTL that encourages models to share information across tasks, for a given covariate, through separately 1) shrinking the coefficient supports together, and/or 2) shrinking the coefficient values together. This allows models to borrow strength during variable selection even when the coefficient values differ markedly between tasks. We express our modeling framework as a Mixed-Integer Program, and propose efficient and scalable algorithms based on block coordinate descent and combinatorial local search. We show our estimator achieves statistically optimal prediction rates. Importantly, our theory characterizes how our estimator leverages the shared support information across tasks to achieve better variable selection performance. We evaluate the performance of our method in simulations and two biology applications. Our proposed approaches outperform other sparse MTL methods in variable selection and prediction accuracy. Interestingly, penalties that shrink the supports together often outperform penalties that shrink the coefficient values together. We will release an R package implementing our methods.

Optimal Ensemble Construction for Multi-Study Prediction with Applications to COVID-19 Excess Mortality Estimation

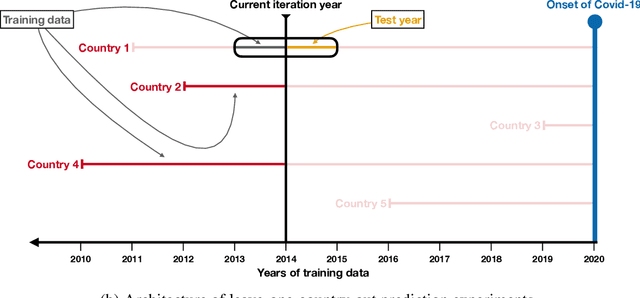
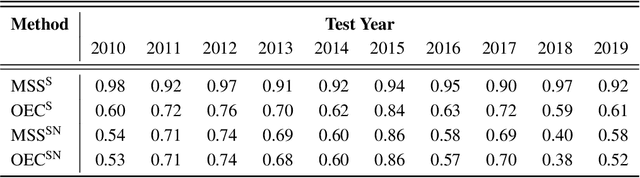
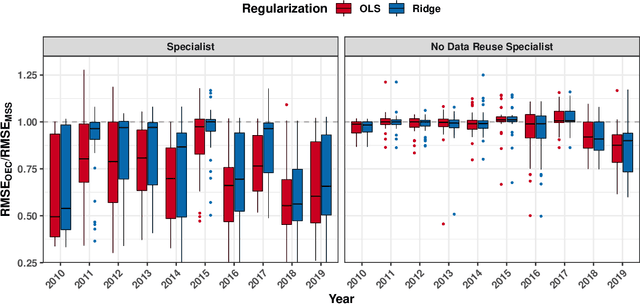
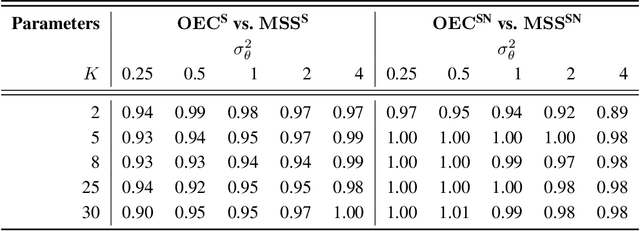
It is increasingly common to encounter prediction tasks in the biomedical sciences for which multiple datasets are available for model training. Common approaches such as pooling datasets and applying standard statistical learning methods can result in poor out-of-study prediction performance when datasets are heterogeneous. Theoretical and applied work has shown $\textit{multi-study ensembling}$ to be a viable alternative that leverages the variability across datasets in a manner that promotes model generalizability. Multi-study ensembling uses a two-stage $\textit{stacking}$ strategy which fits study-specific models and estimates ensemble weights separately. This approach ignores, however, the ensemble properties at the model-fitting stage, potentially resulting in a loss of efficiency. We therefore propose $\textit{optimal ensemble construction}$, an $\textit{all-in-one}$ approach to multi-study stacking whereby we jointly estimate ensemble weights as well as parameters associated with each study-specific model. We prove that limiting cases of our approach yield existing methods such as multi-study stacking and pooling datasets before model fitting. We propose an efficient block coordinate descent algorithm to optimize the proposed loss function. We compare our approach to standard methods by applying it to a multi-country COVID-19 dataset for baseline mortality prediction. We show that when little data is available for a country before the onset of the pandemic, leveraging data from other countries can substantially improve prediction accuracy. Importantly, our approach outperforms multi-study stacking and other standard methods in this application. We further characterize the method's performance in simulations. Our method remains competitive with or outperforms multi-study stacking and other earlier methods across a range of between-study heterogeneity levels.