Kenneth T. Kishida
Multi-Task Learning for Sparsity Pattern Heterogeneity: A Discrete Optimization Approach
Dec 16, 2022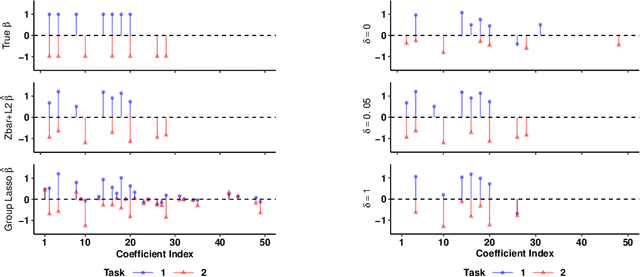

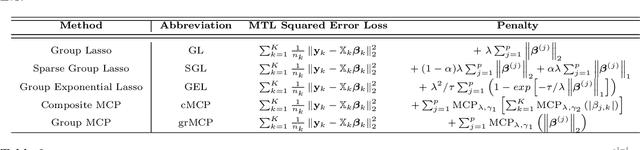
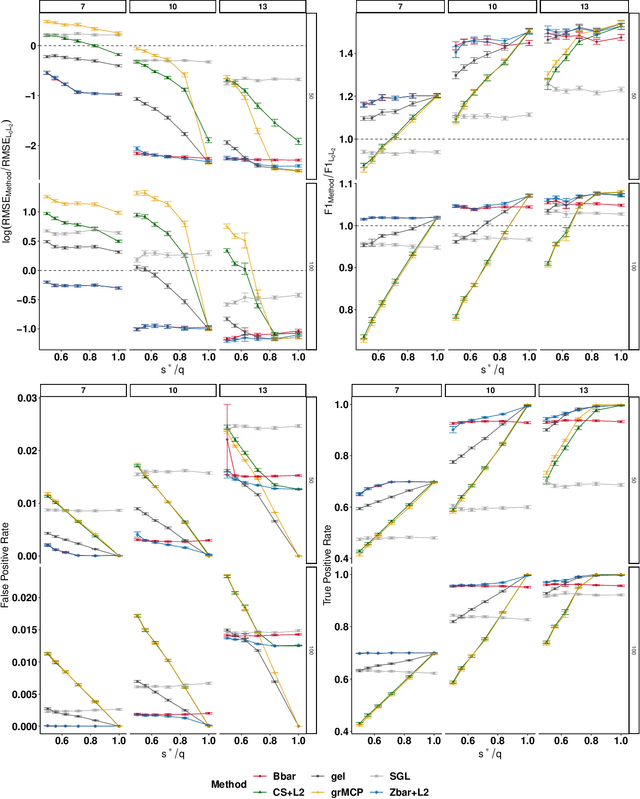
Abstract:We extend best-subset selection to linear Multi-Task Learning (MTL), where a set of linear models are jointly trained on a collection of datasets (``tasks''). Allowing the regression coefficients of tasks to have different sparsity patterns (i.e., different supports), we propose a modeling framework for MTL that encourages models to share information across tasks, for a given covariate, through separately 1) shrinking the coefficient supports together, and/or 2) shrinking the coefficient values together. This allows models to borrow strength during variable selection even when the coefficient values differ markedly between tasks. We express our modeling framework as a Mixed-Integer Program, and propose efficient and scalable algorithms based on block coordinate descent and combinatorial local search. We show our estimator achieves statistically optimal prediction rates. Importantly, our theory characterizes how our estimator leverages the shared support information across tasks to achieve better variable selection performance. We evaluate the performance of our method in simulations and two biology applications. Our proposed approaches outperform other sparse MTL methods in variable selection and prediction accuracy. Interestingly, penalties that shrink the supports together often outperform penalties that shrink the coefficient values together. We will release an R package implementing our methods.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge