LEARNER: A Transfer Learning Method for Low-Rank Matrix Estimation

Low-rank matrix estimation is a fundamental problem in statistics and machine learning. In the context of heterogeneous data generated from diverse sources, a key challenge lies in leveraging data from a source population to enhance the estimation of a low-rank matrix in a target population of interest. One such example is estimating associations between genetic variants and diseases in non-European ancestry groups. We propose an approach that leverages similarity in the latent row and column spaces between the source and target populations to improve estimation in the target population, which we refer to as LatEnt spAce-based tRaNsfer lEaRning (LEARNER). LEARNER is based on performing a low-rank approximation of the target population data which penalizes differences between the latent row and column spaces between the source and target populations. We present a cross-validation approach that allows the method to adapt to the degree of heterogeneity across populations. We conducted extensive simulations which found that LEARNER often outperforms the benchmark approach that only uses the target population data, especially as the signal-to-noise ratio in the source population increases. We also performed an illustrative application and empirical comparison of LEARNER and benchmark approaches in a re-analysis of a genome-wide association study in the BioBank Japan cohort. LEARNER is implemented in the R package learner.

On Undersmoothing and Sample Splitting for Estimating a Doubly Robust Functional

We consider the problem of constructing minimax rate-optimal estimators for a doubly robust nonparametric functional that has witnessed applications across the causal inference and conditional independence testing literature. Minimax rate-optimal estimators for such functionals are typically constructed through higher-order bias corrections of plug-in and one-step type estimators and, in turn, depend on estimators of nuisance functions. In this paper, we consider a parallel question of interest regarding the optimality and/or sub-optimality of plug-in and one-step bias-corrected estimators for the specific doubly robust functional of interest. Specifically, we verify that by using undersmoothing and sample splitting techniques when constructing nuisance function estimators, one can achieve minimax rates of convergence in all H\"older smoothness classes of the nuisance functions (i.e. the propensity score and outcome regression) provided that the marginal density of the covariates is sufficiently regular. Additionally, by demonstrating suitable lower bounds on these classes of estimators, we demonstrate the necessity to undersmooth the nuisance function estimators to obtain minimax optimal rates of convergence.

When Does Uncertainty Matter?: Understanding the Impact of Predictive Uncertainty in ML Assisted Decision Making

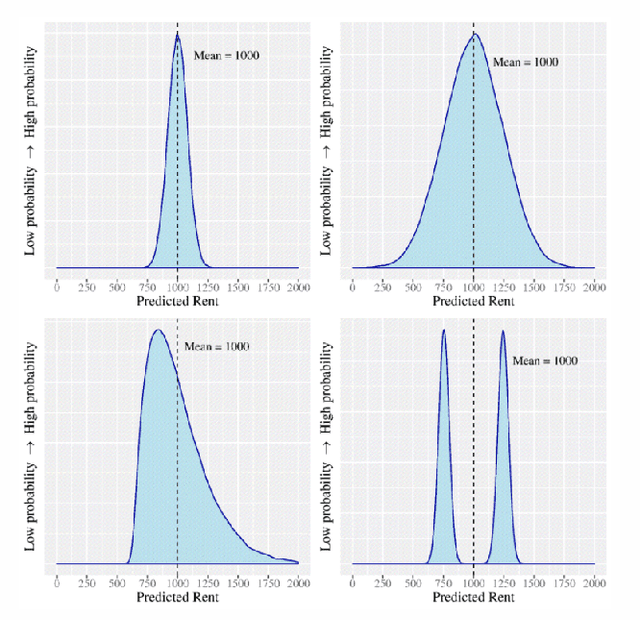
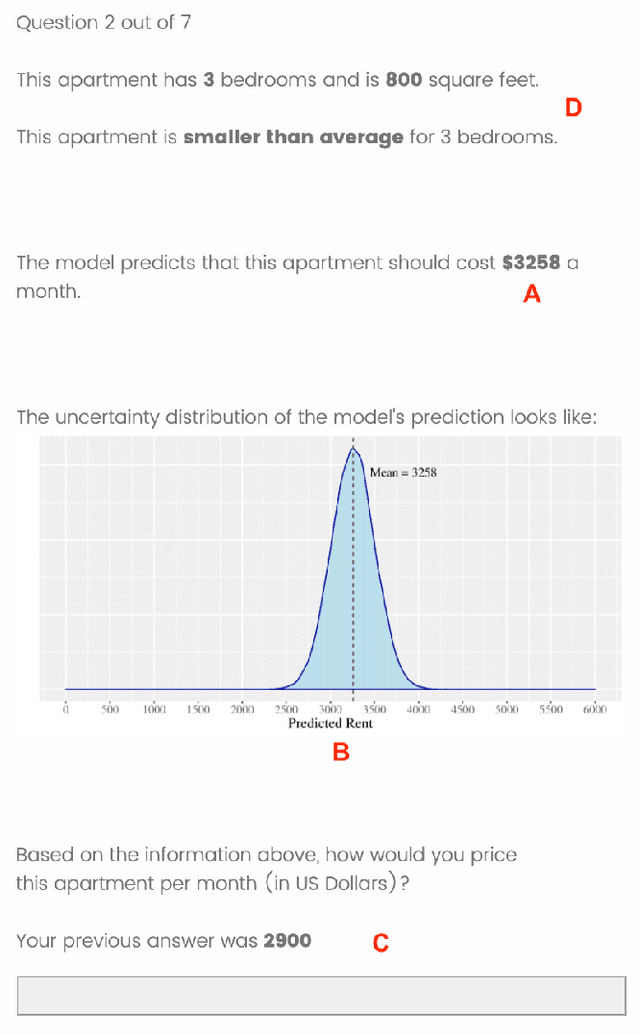
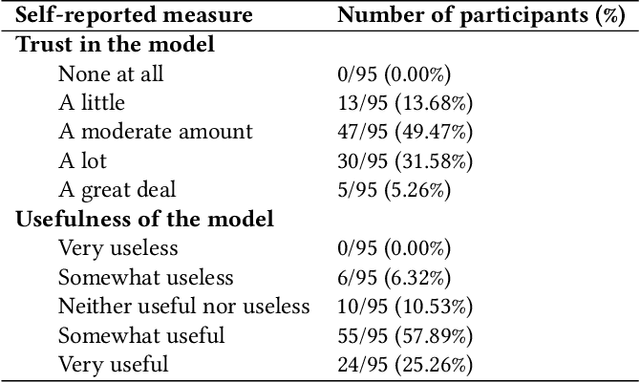
As machine learning (ML) models are increasingly being employed to assist human decision makers, it becomes critical to provide these decision makers with relevant inputs which can help them decide if and how to incorporate model predictions into their decision making. For instance, communicating the uncertainty associated with model predictions could potentially be helpful in this regard. However, there is little to no research that systematically explores if and how conveying predictive uncertainty impacts decision making. In this work, we carry out user studies to systematically assess how people respond to different types of predictive uncertainty i.e., posterior predictive distributions with different shapes and variances, in the context of ML assisted decision making. To the best of our knowledge, this work marks one of the first attempts at studying this question. Our results demonstrate that people are more likely to agree with a model prediction when they observe the corresponding uncertainty associated with the prediction. This finding holds regardless of the properties (shape or variance) of predictive uncertainty (posterior predictive distribution), suggesting that uncertainty is an effective tool for persuading humans to agree with model predictions. Furthermore, we also find that other factors such as domain expertise and familiarity with ML also play a role in determining how someone interprets and incorporates predictive uncertainty into their decision making.