A New Central Limit Theorem for the Augmented IPW Estimator: Variance Inflation, Cross-Fit Covariance and Beyond

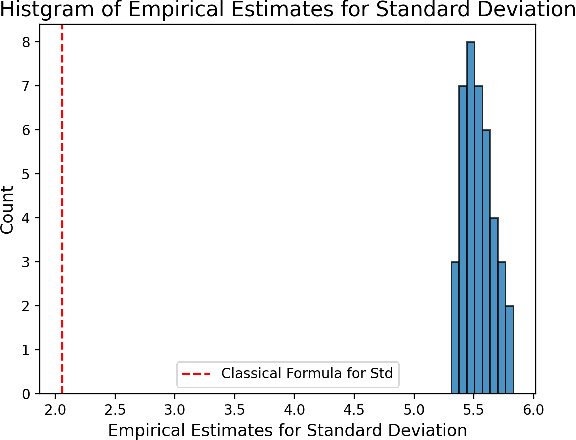
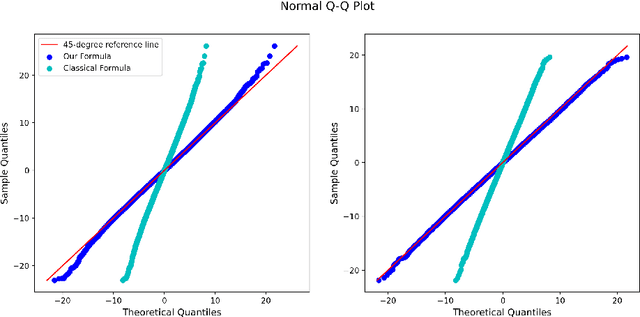
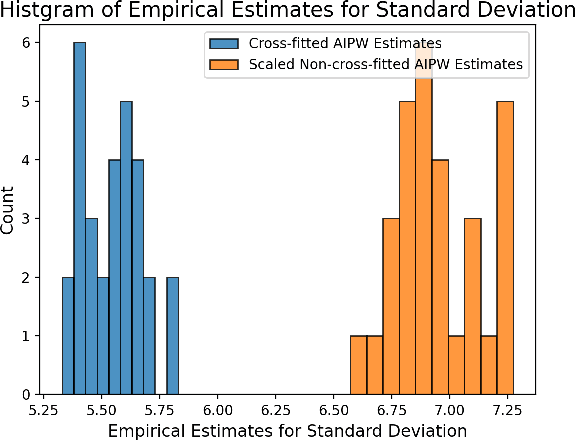
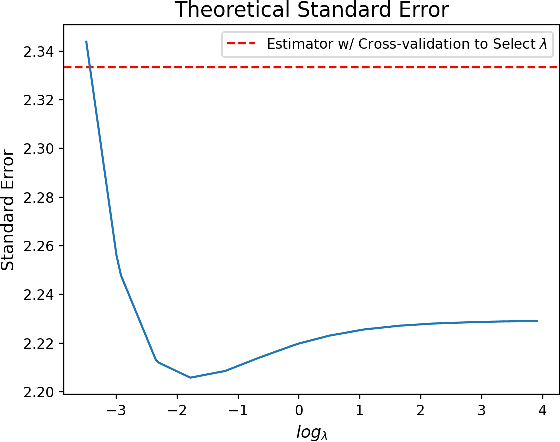
Estimation of the average treatment effect (ATE) is a central problem in causal inference. In recent times, inference for the ATE in the presence of high-dimensional covariates has been extensively studied. Among the diverse approaches that have been proposed, augmented inverse probability weighting (AIPW) with cross-fitting has emerged as a popular choice in practice. In this work, we study this cross-fit AIPW estimator under well-specified outcome regression and propensity score models in a high-dimensional regime where the number of features and samples are both large and comparable. Under assumptions on the covariate distribution, we establish a new CLT for the suitably scaled cross-fit AIPW that applies without any sparsity assumptions on the underlying high-dimensional parameters. Our CLT uncovers two crucial phenomena among others: (i) the AIPW exhibits a substantial variance inflation that can be precisely quantified in terms of the signal-to-noise ratio and other problem parameters, (ii) the asymptotic covariance between the pre-cross-fit estimates is non-negligible even on the root-n scale. In fact, these cross-covariances turn out to be negative in our setting. These findings are strikingly different from their classical counterparts. On the technical front, our work utilizes a novel interplay between three distinct tools--approximate message passing theory, the theory of deterministic equivalents, and the leave-one-out approach. We believe our proof techniques should be useful for analyzing other two-stage estimators in this high-dimensional regime. Finally, we complement our theoretical results with simulations that demonstrate both the finite sample efficacy of our CLT and its robustness to our assumptions.