Discrete Sampling using Semigradient-based Product Mixtures
Paper and Code
Jul 09, 2018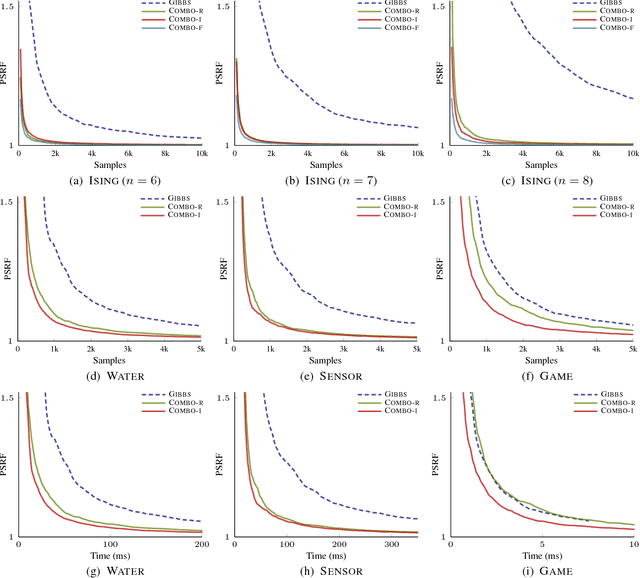
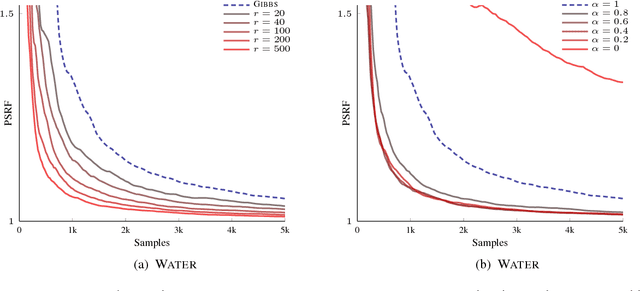
We consider the problem of inference in discrete probabilistic models, that is, distributions over subsets of a finite ground set. These encompass a range of well-known models in machine learning, such as determinantal point processes and Ising models. Locally-moving Markov chain Monte Carlo algorithms, such as the Gibbs sampler, are commonly used for inference in such models, but their convergence is, at times, prohibitively slow. This is often caused by state-space bottlenecks that greatly hinder the movement of such samplers. We propose a novel sampling strategy that uses a specific mixture of product distributions to propose global moves and, thus, accelerate convergence. Furthermore, we show how to construct such a mixture using semigradient information. We illustrate the effectiveness of combining our sampler with existing ones, both theoretically on an example model, as well as practically on three models learned from real-world data sets.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge