On the Fairness of Disentangled Representations

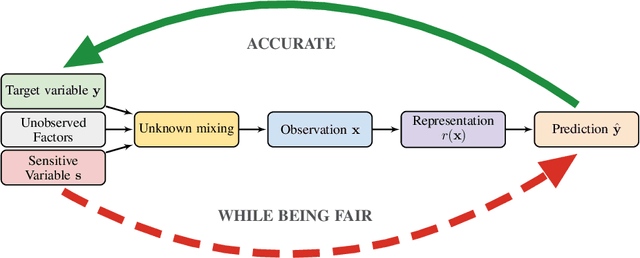
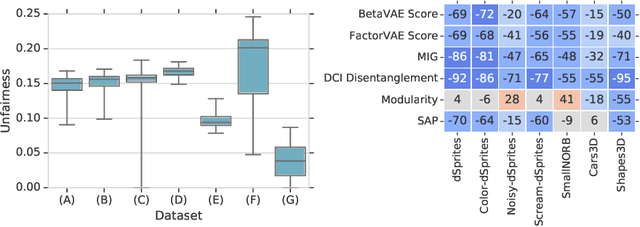
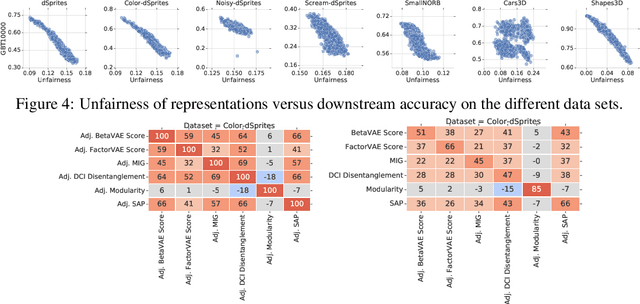
Recently there has been a significant interest in learning disentangled representations, as they promise increased interpretability, generalization to unseen scenarios and faster learning on downstream tasks. In this paper, we investigate the usefulness of different notions of disentanglement for improving the fairness of downstream prediction tasks based on representations. We consider the setting where the goal is to predict a target variable based on the learned representation of high-dimensional observations (such as images) that depend on both the target variable and an unobserved sensitive variable. We show that in this setting both the optimal and empirical predictions can be unfair, even if the target variable and the sensitive variable are independent. Analyzing more than 12600 trained representations of state-of-the-art disentangled models, we observe that various disentanglement scores are consistently correlated with increased fairness, suggesting that disentanglement may be a useful property to encourage fairness when sensitive variables are not observed.

AReS and MaRS - Adversarial and MMD-Minimizing Regression for SDEs

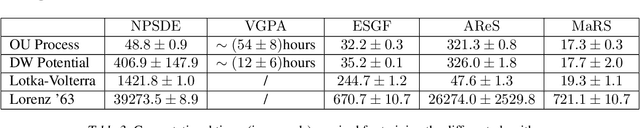
Stochastic differential equations are an important modeling class in many disciplines. Consequently, there exist many methods relying on various discretization and numerical integration schemes. In this paper, we propose a novel, probabilistic model for estimating the drift and diffusion given noisy observations of the underlying stochastic system. Using state-of-the-art adversarial and moment matching inference techniques, we circumvent the use of the discretization schemes as seen in classical approaches. This yields significant improvements in parameter estimation accuracy and robustness given random initial guesses. On four commonly used benchmark systems, we demonstrate the performance of our algorithms compared to state-of-the-art solutions based on extended Kalman filtering and Gaussian processes.

ODIN: ODE-Informed Regression for Parameter and State Inference in Time-Continuous Dynamical Systems

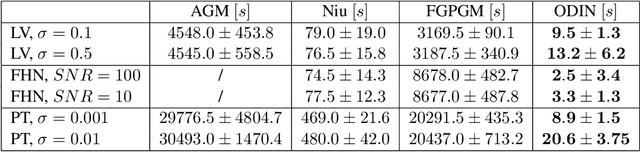
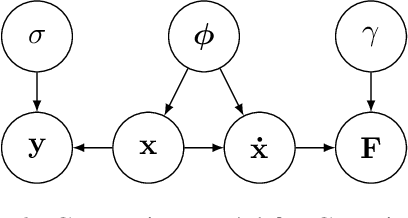
Parameter inference in ordinary differential equations is an important problem in many applied sciences and in engineering, especially in a data-scarce setting. In this work, we introduce a novel generative modeling approach based on constrained Gaussian processes and use it to create a computationally and data efficient algorithm for state and parameter inference. In an extensive set of experiments, our approach outperforms its competitors both in terms of accuracy and computational cost for parameter inference. It also shows promising results for the much more challenging problem of model selection.

MOrdReD: Memory-based Ordinal Regression Deep Neural Networks for Time Series Forecasting

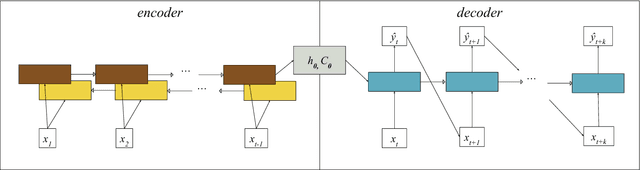
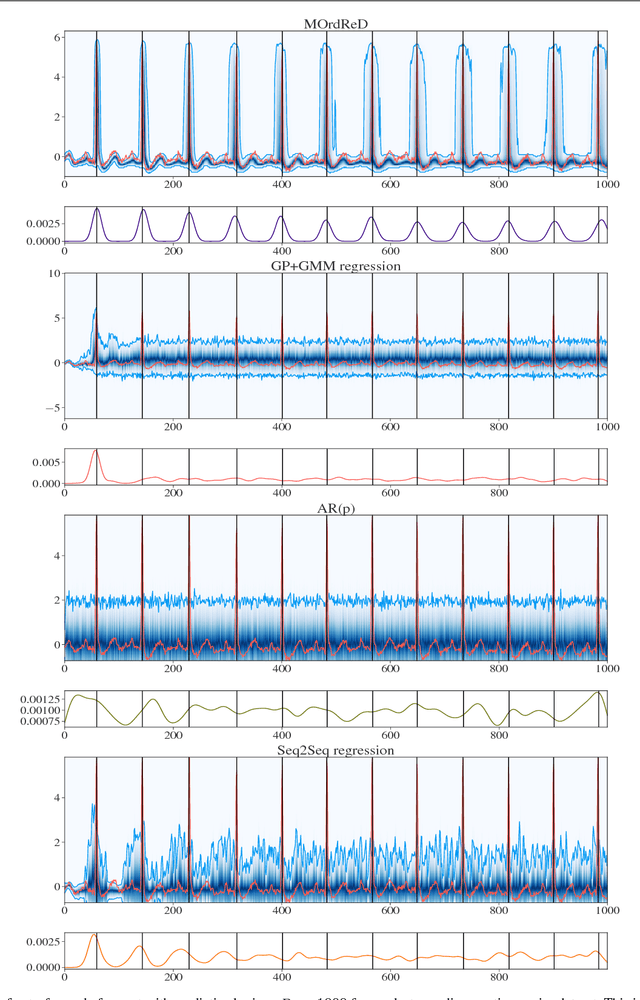
Time series forecasting is ubiquitous in the modern world. Applications range from health care to astronomy, and include climate modelling, financial trading and monitoring of critical engineering equipment. To offer value over this range of activities, models must not only provide accurate forecasts, but also quantify and adjust their uncertainty over time. In this work, we directly tackle this task with a novel, fully end-to-end deep learning method for time series forecasting. By recasting time series forecasting as an ordinal regression task, we develop a principled methodology to assess long-term predictive uncertainty and describe rich multimodal, non-Gaussian behaviour, which arises regularly in applied settings. Notably, our framework is a wholly general-purpose approach that requires little to no user intervention to be used. We showcase this key feature in a large-scale benchmark test with 45 datasets drawn from both, a wide range of real-world application domains, as well as a comprehensive list of synthetic maps. This wide comparison encompasses state-of-the-art methods in both the Machine Learning and Statistics modelling literature, such as the Gaussian Process. We find that our approach does not only provide excellent predictive forecasts, shadowing true future values, but also allows us to infer valuable information, such as the predictive distribution of the occurrence of critical events of interest, accurately and reliably even over long time horizons.