MOrdReD: Memory-based Ordinal Regression Deep Neural Networks for Time Series Forecasting
Paper and Code
Oct 24, 2018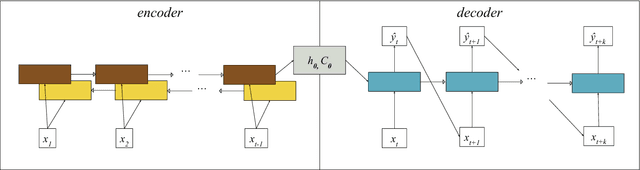


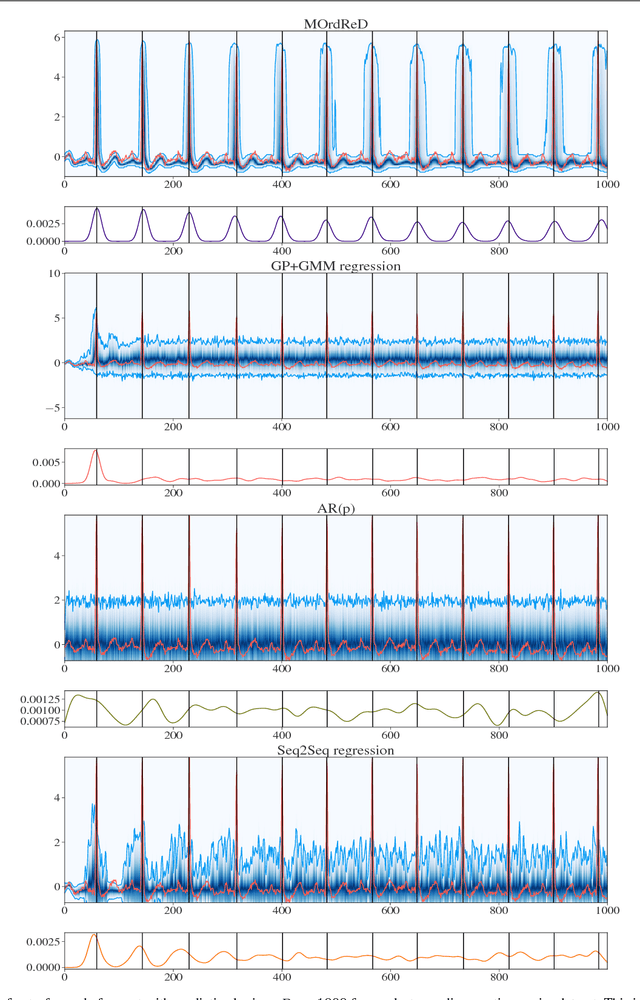
Time series forecasting is ubiquitous in the modern world. Applications range from health care to astronomy, and include climate modelling, financial trading and monitoring of critical engineering equipment. To offer value over this range of activities, models must not only provide accurate forecasts, but also quantify and adjust their uncertainty over time. In this work, we directly tackle this task with a novel, fully end-to-end deep learning method for time series forecasting. By recasting time series forecasting as an ordinal regression task, we develop a principled methodology to assess long-term predictive uncertainty and describe rich multimodal, non-Gaussian behaviour, which arises regularly in applied settings. Notably, our framework is a wholly general-purpose approach that requires little to no user intervention to be used. We showcase this key feature in a large-scale benchmark test with 45 datasets drawn from both, a wide range of real-world application domains, as well as a comprehensive list of synthetic maps. This wide comparison encompasses state-of-the-art methods in both the Machine Learning and Statistics modelling literature, such as the Gaussian Process. We find that our approach does not only provide excellent predictive forecasts, shadowing true future values, but also allows us to infer valuable information, such as the predictive distribution of the occurrence of critical events of interest, accurately and reliably even over long time horizons.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge