Learning Stable Deep Dynamics Models for Partially Observed or Delayed Dynamical Systems
Paper and Code
Oct 27, 2021

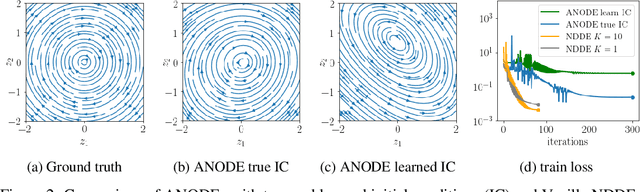
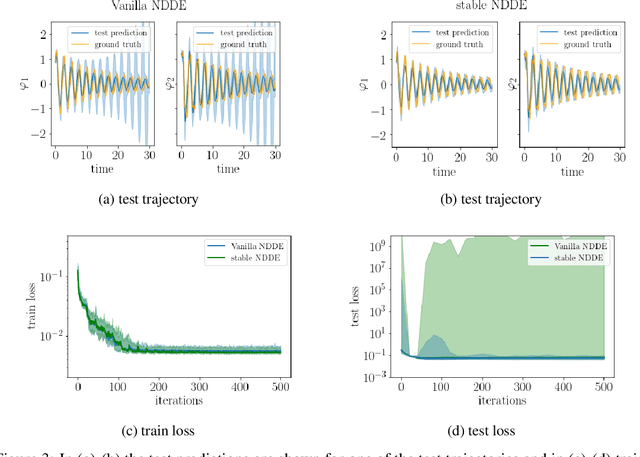
Learning how complex dynamical systems evolve over time is a key challenge in system identification. For safety critical systems, it is often crucial that the learned model is guaranteed to converge to some equilibrium point. To this end, neural ODEs regularized with neural Lyapunov functions are a promising approach when states are fully observed. For practical applications however, partial observations are the norm. As we will demonstrate, initialization of unobserved augmented states can become a key problem for neural ODEs. To alleviate this issue, we propose to augment the system's state with its history. Inspired by state augmentation in discrete-time systems, we thus obtain neural delay differential equations. Based on classical time delay stability analysis, we then show how to ensure stability of the learned models, and theoretically analyze our approach. Our experiments demonstrate its applicability to stable system identification of partially observed systems and learning a stabilizing feedback policy in delayed feedback control.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge