Towards the Transferability of Rewards Recovered via Regularized Inverse Reinforcement Learning

Inverse reinforcement learning (IRL) aims to infer a reward from expert demonstrations, motivated by the idea that the reward, rather than the policy, is the most succinct and transferable description of a task [Ng et al., 2000]. However, the reward corresponding to an optimal policy is not unique, making it unclear if an IRL-learned reward is transferable to new transition laws in the sense that its optimal policy aligns with the optimal policy corresponding to the expert's true reward. Past work has addressed this problem only under the assumption of full access to the expert's policy, guaranteeing transferability when learning from two experts with the same reward but different transition laws that satisfy a specific rank condition [Rolland et al., 2022]. In this work, we show that the conditions developed under full access to the expert's policy cannot guarantee transferability in the more practical scenario where we have access only to demonstrations of the expert. Instead of a binary rank condition, we propose principal angles as a more refined measure of similarity and dissimilarity between transition laws. Based on this, we then establish two key results: 1) a sufficient condition for transferability to any transition laws when learning from at least two experts with sufficiently different transition laws, and 2) a sufficient condition for transferability to local changes in the transition law when learning from a single expert. Furthermore, we also provide a probably approximately correct (PAC) algorithm and an end-to-end analysis for learning transferable rewards from demonstrations of multiple experts.

Convergence of a model-free entropy-regularized inverse reinforcement learning algorithm

Given a dataset of expert demonstrations, inverse reinforcement learning (IRL) aims to recover a reward for which the expert is optimal. This work proposes a model-free algorithm to solve entropy-regularized IRL problem. In particular, we employ a stochastic gradient descent update for the reward and a stochastic soft policy iteration update for the policy. Assuming access to a generative model, we prove that our algorithm is guaranteed to recover a reward for which the expert is $\varepsilon$-optimal using $\mathcal{O}(1/\varepsilon^{2})$ samples of the Markov decision process (MDP). Furthermore, with $\mathcal{O}(1/\varepsilon^{4})$ samples we prove that the optimal policy corresponding to the recovered reward is $\varepsilon$-close to the expert policy in total variation distance.

Identifiability and Generalizability in Constrained Inverse Reinforcement Learning

Two main challenges in Reinforcement Learning (RL) are designing appropriate reward functions and ensuring the safety of the learned policy. To address these challenges, we present a theoretical framework for Inverse Reinforcement Learning (IRL) in constrained Markov decision processes. From a convex-analytic perspective, we extend prior results on reward identifiability and generalizability to both the constrained setting and a more general class of regularizations. In particular, we show that identifiability up to potential shaping (Cao et al., 2021) is a consequence of entropy regularization and may generally no longer hold for other regularizations or in the presence of safety constraints. We also show that to ensure generalizability to new transition laws and constraints, the true reward must be identified up to a constant. Additionally, we derive a finite sample guarantee for the suboptimality of the learned rewards, and validate our results in a gridworld environment.

Learning Stable Deep Dynamics Models for Partially Observed or Delayed Dynamical Systems

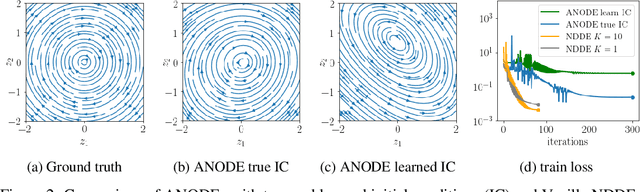
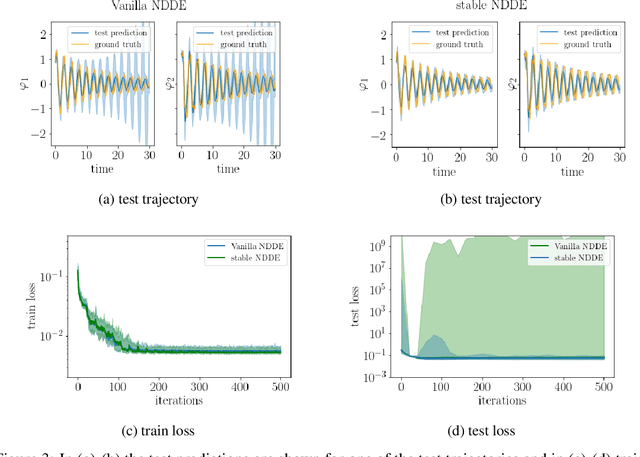
Learning how complex dynamical systems evolve over time is a key challenge in system identification. For safety critical systems, it is often crucial that the learned model is guaranteed to converge to some equilibrium point. To this end, neural ODEs regularized with neural Lyapunov functions are a promising approach when states are fully observed. For practical applications however, partial observations are the norm. As we will demonstrate, initialization of unobserved augmented states can become a key problem for neural ODEs. To alleviate this issue, we propose to augment the system's state with its history. Inspired by state augmentation in discrete-time systems, we thus obtain neural delay differential equations. Based on classical time delay stability analysis, we then show how to ensure stability of the learned models, and theoretically analyze our approach. Our experiments demonstrate its applicability to stable system identification of partially observed systems and learning a stabilizing feedback policy in delayed feedback control.