Model-Based Learning of Near-Optimal Finite-Window Policies in POMDPs

We study model-based learning of finite-window policies in tabular partially observable Markov decision processes (POMDPs). A common approach to learning under partial observability is to approximate unbounded history dependencies using finite action-observation windows. This induces a finite-state Markov decision process (MDP) over histories, referred to as the superstate MDP. Once a model of this superstate MDP is available, standard MDP algorithms can be used to compute optimal policies, motivating the need for sample-efficient model estimation. Estimating the superstate MDP model is challenging because trajectories are generated by interaction with the original POMDP, creating a mismatch between the sampling process and target model. We propose a model estimation procedure for tabular POMDPs and analyze its sample complexity. Our analysis exploits a connection between filter stability and concentration inequalities for weakly dependent random variables. As a result, we obtain tight sample complexity guarantees for estimating the superstate MDP model from a single trajectory. Combined with value iteration, this yields approximately optimal finite-window policies for the POMDP.

Constrained Meta Reinforcement Learning with Provable Test-Time Safety

Meta reinforcement learning (RL) allows agents to leverage experience across a distribution of tasks on which the agent can train at will, enabling faster learning of optimal policies on new test tasks. Despite its success in improving sample complexity on test tasks, many real-world applications, such as robotics and healthcare, impose safety constraints during testing. Constrained meta RL provides a promising framework for integrating safety into meta RL. An open question in constrained meta RL is how to ensure the safety of the policy on the real-world test task, while reducing the sample complexity and thus, enabling faster learning of optimal policies. To address this gap, we propose an algorithm that refines policies learned during training, with provable safety and sample complexity guarantees for learning a near optimal policy on the test tasks. We further derive a matching lower bound, showing that this sample complexity is tight.

Identifying Time-varying Costs in Finite-horizon Linear Quadratic Gaussian Games

We address cost identification in a finite-horizon linear quadratic Gaussian game. We characterize the set of cost parameters that generate a given Nash equilibrium policy. We propose a backpropagation algorithm to identify the time-varying cost parameters. We derive a probabilistic error bound when the cost parameters are identified from finite trajectories. We test our method in numerical and driving simulations. Our algorithm identifies the cost parameters that can reproduce the Nash equilibrium policy and trajectory observations.

Nash Equilibria in Games with Playerwise Concave Coupling Constraints: Existence and Computation

We study the existence and computation of Nash equilibria in continuous static games where the players' admissible strategies are subject to shared coupling constraints, i.e., constraints that depend on their \emph{joint} strategies. Specifically, we focus on a class of games characterized by playerwise concave utilities and playerwise concave constraints. Prior results on the existence of Nash equilibria are not applicable to this class, as they rely on strong assumptions such as joint convexity of the feasible set. By leveraging topological fixed point theory and novel structural insights into the contractibility of feasible sets under playerwise concave constraints, we give an existence proof for Nash equilibria under weaker conditions. Having established existence, we then focus on the computation of Nash equilibria via independent gradient methods under the additional assumption that the utilities admit a potential function. To account for the possibly nonconvex feasible region, we employ a log barrier regularized gradient ascent with adaptive stepsizes. Starting from an initial feasible strategy profile and under exact gradient feedback, the proposed method converges to an $\epsilon$-approximate constrained Nash equilibrium within $\mathcal{O}(\epsilon^{-3})$ iterations.

Chance-constrained Linear Quadratic Gaussian Games for Multi-robot Interaction under Uncertainty

We address safe multi-robot interaction under uncertainty. In particular, we formulate a chance-constrained linear quadratic Gaussian game with coupling constraints and system uncertainties. We find a tractable reformulation of the game and propose a dual ascent algorithm. We prove that the algorithm converges to a generalized Nash equilibrium of the reformulated game, ensuring the satisfaction of the chance constraints. We test our method in driving simulations and real-world robot experiments. Our method ensures safety under uncertainty and generates less conservative trajectories than single-agent model predictive control.

Chance-Constrained Trajectory Planning with Multimodal Environmental Uncertainty

We tackle safe trajectory planning under Gaussian mixture model (GMM) uncertainty. Specifically, we use a GMM to model the multimodal behaviors of obstacles' uncertain states. Then, we develop a mixed-integer conic approximation to the chance-constrained trajectory planning problem with deterministic linear systems and polyhedral obstacles. When the GMM moments are estimated via finite samples, we develop a tight concentration bound to ensure the chance constraint with a desired confidence. Moreover, to limit the amount of constraint violation, we develop a Conditional Value-at-Risk (CVaR) approach corresponding to the chance constraints and derive a tractable approximation for known and estimated GMM moments. We verify our methods with state-of-the-art trajectory prediction algorithms and autonomous driving datasets.

A learning-based approach to stochastic optimal control under reach-avoid constraint

We develop a model-free approach to optimally control stochastic, Markovian systems subject to a reach-avoid constraint. Specifically, the state trajectory must remain within a safe set while reaching a target set within a finite time horizon. Due to the time-dependent nature of these constraints, we show that, in general, the optimal policy for this constrained stochastic control problem is non-Markovian, which increases the computational complexity. To address this challenge, we apply the state-augmentation technique from arXiv:2402.19360, reformulating the problem as a constrained Markov decision process (CMDP) on an extended state space. This transformation allows us to search for a Markovian policy, avoiding the complexity of non-Markovian policies. To learn the optimal policy without a system model, and using only trajectory data, we develop a log-barrier policy gradient approach. We prove that under suitable assumptions, the policy parameters converge to the optimal parameters, while ensuring that the system trajectories satisfy the stochastic reach-avoid constraint with high probability.

Towards the Transferability of Rewards Recovered via Regularized Inverse Reinforcement Learning

Inverse reinforcement learning (IRL) aims to infer a reward from expert demonstrations, motivated by the idea that the reward, rather than the policy, is the most succinct and transferable description of a task [Ng et al., 2000]. However, the reward corresponding to an optimal policy is not unique, making it unclear if an IRL-learned reward is transferable to new transition laws in the sense that its optimal policy aligns with the optimal policy corresponding to the expert's true reward. Past work has addressed this problem only under the assumption of full access to the expert's policy, guaranteeing transferability when learning from two experts with the same reward but different transition laws that satisfy a specific rank condition [Rolland et al., 2022]. In this work, we show that the conditions developed under full access to the expert's policy cannot guarantee transferability in the more practical scenario where we have access only to demonstrations of the expert. Instead of a binary rank condition, we propose principal angles as a more refined measure of similarity and dissimilarity between transition laws. Based on this, we then establish two key results: 1) a sufficient condition for transferability to any transition laws when learning from at least two experts with sufficiently different transition laws, and 2) a sufficient condition for transferability to local changes in the transition law when learning from a single expert. Furthermore, we also provide a probably approximately correct (PAC) algorithm and an end-to-end analysis for learning transferable rewards from demonstrations of multiple experts.

Convergence of a model-free entropy-regularized inverse reinforcement learning algorithm

Given a dataset of expert demonstrations, inverse reinforcement learning (IRL) aims to recover a reward for which the expert is optimal. This work proposes a model-free algorithm to solve entropy-regularized IRL problem. In particular, we employ a stochastic gradient descent update for the reward and a stochastic soft policy iteration update for the policy. Assuming access to a generative model, we prove that our algorithm is guaranteed to recover a reward for which the expert is $\varepsilon$-optimal using $\mathcal{O}(1/\varepsilon^{2})$ samples of the Markov decision process (MDP). Furthermore, with $\mathcal{O}(1/\varepsilon^{4})$ samples we prove that the optimal policy corresponding to the recovered reward is $\varepsilon$-close to the expert policy in total variation distance.

Learning Nash Equilibria in Zero-Sum Markov Games: A Single Time-scale Algorithm Under Weak Reachability

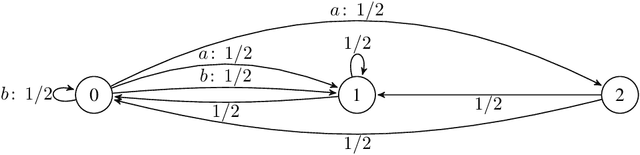
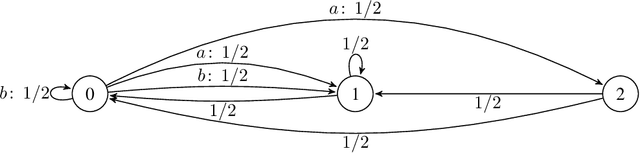
We consider decentralized learning for zero-sum games, where players only see their payoff information and are agnostic to actions and payoffs of the opponent. Previous works demonstrated convergence to a Nash equilibrium in this setting using double time-scale algorithms under strong reachability assumptions. We address the open problem of achieving an approximate Nash equilibrium efficiently with an uncoupled and single time-scale algorithm under weaker conditions. Our contribution is a rational and convergent algorithm, utilizing Tsallis-entropy regularization in a value-iteration-based approach. The algorithm learns an approximate Nash equilibrium in polynomial time, requiring only the existence of a policy pair that induces an irreducible and aperiodic Markov chain, thus considerably weakening past assumptions. Our analysis leverages negative drift inequalities and introduces novel properties of Tsallis entropy that are of independent interest.