Learning Nash Equilibria in Zero-Sum Markov Games: A Single Time-scale Algorithm Under Weak Reachability

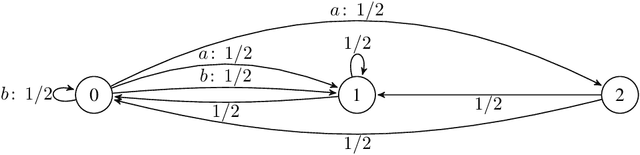
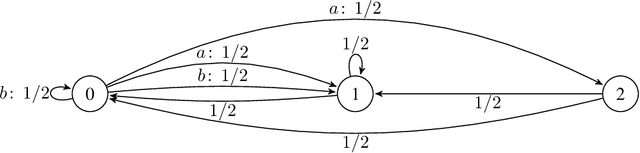
We consider decentralized learning for zero-sum games, where players only see their payoff information and are agnostic to actions and payoffs of the opponent. Previous works demonstrated convergence to a Nash equilibrium in this setting using double time-scale algorithms under strong reachability assumptions. We address the open problem of achieving an approximate Nash equilibrium efficiently with an uncoupled and single time-scale algorithm under weaker conditions. Our contribution is a rational and convergent algorithm, utilizing Tsallis-entropy regularization in a value-iteration-based approach. The algorithm learns an approximate Nash equilibrium in polynomial time, requiring only the existence of a policy pair that induces an irreducible and aperiodic Markov chain, thus considerably weakening past assumptions. Our analysis leverages negative drift inequalities and introduces novel properties of Tsallis entropy that are of independent interest.

Bilinear Exponential Family of MDPs: Frequentist Regret Bound with Tractable Exploration and Planning

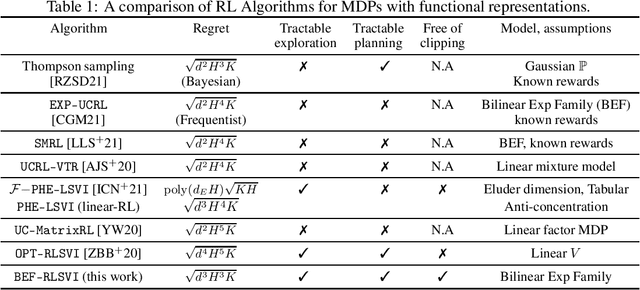
We study the problem of episodic reinforcement learning in continuous state-action spaces with unknown rewards and transitions. Specifically, we consider the setting where the rewards and transitions are modeled using parametric bilinear exponential families. We propose an algorithm, BEF-RLSVI, that a) uses penalized maximum likelihood estimators to learn the unknown parameters, b) injects a calibrated Gaussian noise in the parameter of rewards to ensure exploration, and c) leverages linearity of the exponential family with respect to an underlying RKHS to perform tractable planning. We further provide a frequentist regret analysis of BEF-RLSVI that yields an upper bound of $\tilde{\mathcal{O}}(\sqrt{d^3H^3K})$, where $d$ is the dimension of the parameters, $H$ is the episode length, and $K$ is the number of episodes. Our analysis improves the existing bounds for the bilinear exponential family of MDPs by $\sqrt{H}$ and removes the handcrafted clipping deployed in existing \RLSVI-type algorithms. Our regret bound is order-optimal with respect to $H$ and $K$.

Stochastic Online Linear Regression: the Forward Algorithm to Replace Ridge

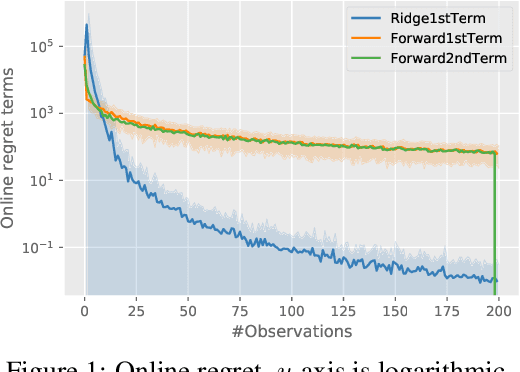
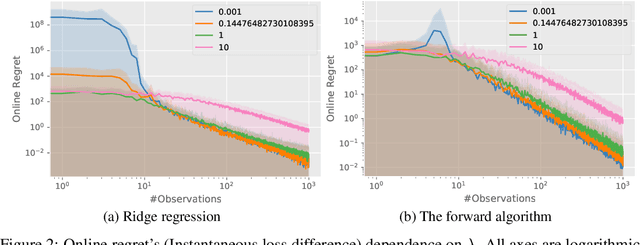
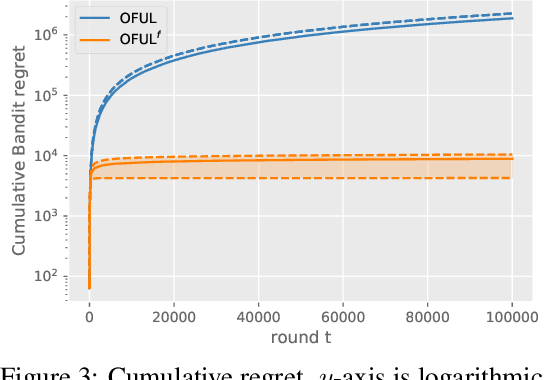
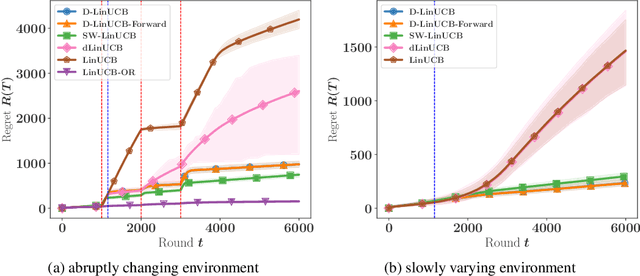
We consider the problem of online linear regression in the stochastic setting. We derive high probability regret bounds for online ridge regression and the forward algorithm. This enables us to compare online regression algorithms more accurately and eliminate assumptions of bounded observations and predictions. Our study advocates for the use of the forward algorithm in lieu of ridge due to its enhanced bounds and robustness to the regularization parameter. Moreover, we explain how to integrate it in algorithms involving linear function approximation to remove a boundedness assumption without deteriorating theoretical bounds. We showcase this modification in linear bandit settings where it yields improved regret bounds. Last, we provide numerical experiments to illustrate our results and endorse our intuitions.

Online Sign Identification: Minimization of the Number of Errors in Thresholding Bandits

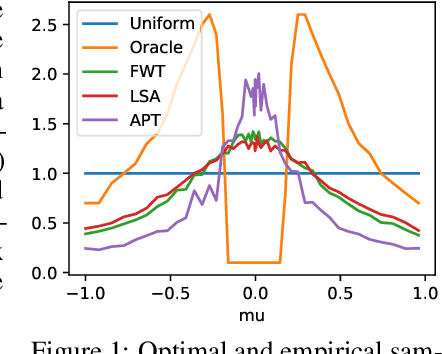
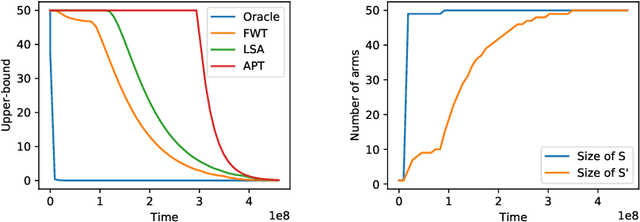
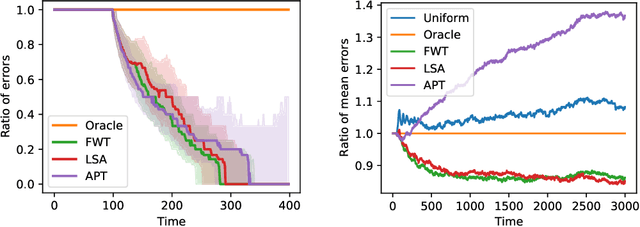
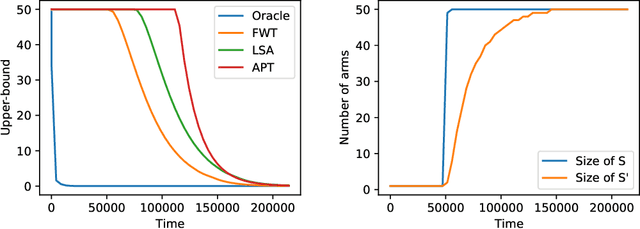
In the fixed budget thresholding bandit problem, an algorithm sequentially allocates a budgeted number of samples to different distributions. It then predicts whether the mean of each distribution is larger or lower than a given threshold. We introduce a large family of algorithms (containing most existing relevant ones), inspired by the Frank-Wolfe algorithm, and provide a thorough yet generic analysis of their performance. This allowed us to construct new explicit algorithms, for a broad class of problems, whose losses are within a small constant factor of the non-adaptive oracle ones. Quite interestingly, we observed that adaptive methods empirically greatly out-perform non-adaptive oracles, an uncommon behavior in standard online learning settings, such as regret minimization. We explain this surprising phenomenon on an insightful toy problem.

Is Standard Deviation the New Standard? Revisiting the Critic in Deep Policy Gradients

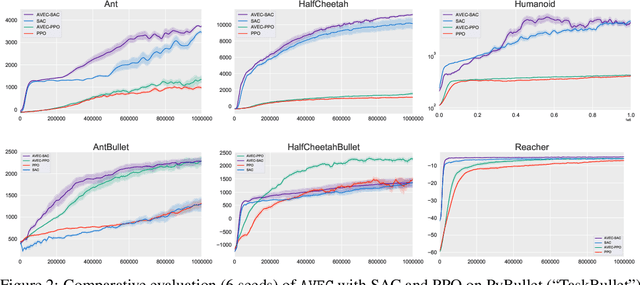
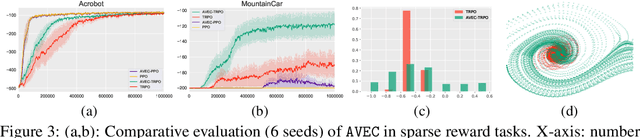
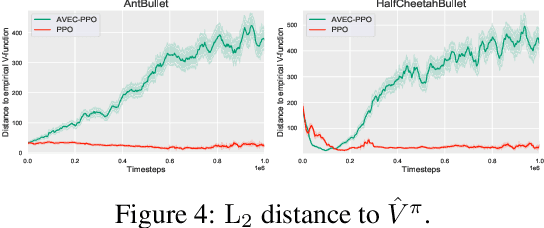
Policy gradient algorithms have proven to be successful in diverse decision making and control tasks. However, these methods suffer from high sample complexity and instability issues. In this paper, we address these challenges by providing a different approach for training the critic in the actor-critic framework. Our work builds on recent studies indicating that traditional actor-critic algorithms do not succeed in fitting the true value function, calling for the need to identify a better objective for the critic. In our method, the critic uses a new state-value (resp. state-action-value) function approximation that learns the relative value of the states (resp. state-action pairs) rather than their absolute value as in conventional actor-critic. We prove the theoretical consistency of the new gradient estimator and observe dramatic empirical improvement across a variety of continuous control tasks and algorithms. Furthermore, we validate our method in tasks with sparse rewards, where we provide experimental evidence and theoretical insights.