Bilinear Exponential Family of MDPs: Frequentist Regret Bound with Tractable Exploration and Planning
Paper and Code
Oct 05, 2022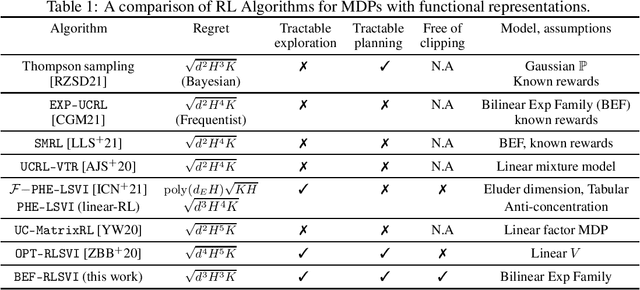

We study the problem of episodic reinforcement learning in continuous state-action spaces with unknown rewards and transitions. Specifically, we consider the setting where the rewards and transitions are modeled using parametric bilinear exponential families. We propose an algorithm, BEF-RLSVI, that a) uses penalized maximum likelihood estimators to learn the unknown parameters, b) injects a calibrated Gaussian noise in the parameter of rewards to ensure exploration, and c) leverages linearity of the exponential family with respect to an underlying RKHS to perform tractable planning. We further provide a frequentist regret analysis of BEF-RLSVI that yields an upper bound of $\tilde{\mathcal{O}}(\sqrt{d^3H^3K})$, where $d$ is the dimension of the parameters, $H$ is the episode length, and $K$ is the number of episodes. Our analysis improves the existing bounds for the bilinear exponential family of MDPs by $\sqrt{H}$ and removes the handcrafted clipping deployed in existing \RLSVI-type algorithms. Our regret bound is order-optimal with respect to $H$ and $K$.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge