Online Sign Identification: Minimization of the Number of Errors in Thresholding Bandits
Paper and Code
Oct 18, 2021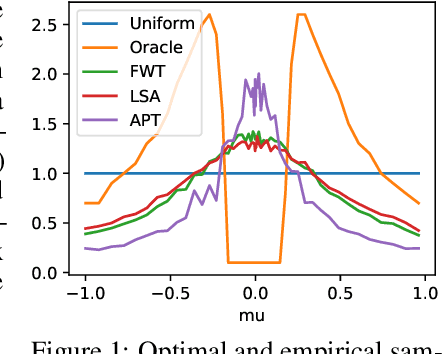
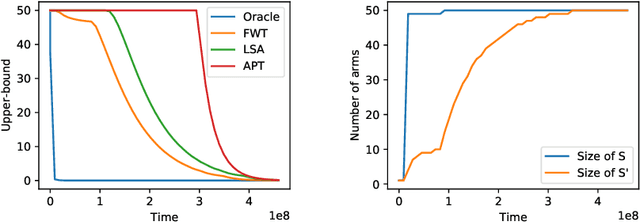
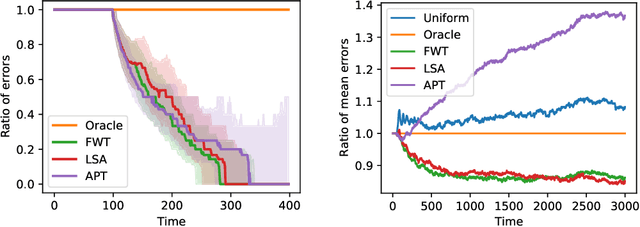
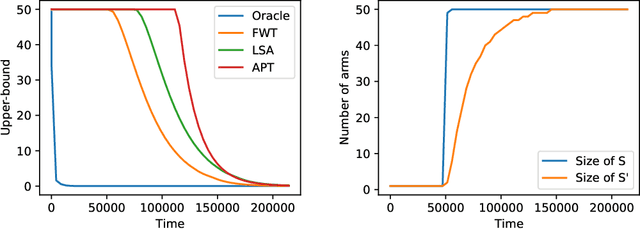
In the fixed budget thresholding bandit problem, an algorithm sequentially allocates a budgeted number of samples to different distributions. It then predicts whether the mean of each distribution is larger or lower than a given threshold. We introduce a large family of algorithms (containing most existing relevant ones), inspired by the Frank-Wolfe algorithm, and provide a thorough yet generic analysis of their performance. This allowed us to construct new explicit algorithms, for a broad class of problems, whose losses are within a small constant factor of the non-adaptive oracle ones. Quite interestingly, we observed that adaptive methods empirically greatly out-perform non-adaptive oracles, an uncommon behavior in standard online learning settings, such as regret minimization. We explain this surprising phenomenon on an insightful toy problem.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge