SLEIPNIR: Deterministic and Provably Accurate Feature Expansion for Gaussian Process Regression with Derivatives
Paper and Code
Mar 05, 2020
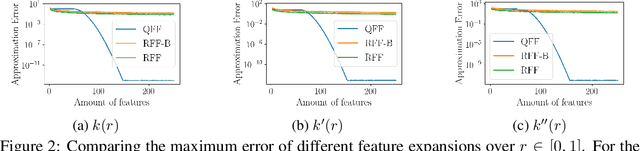
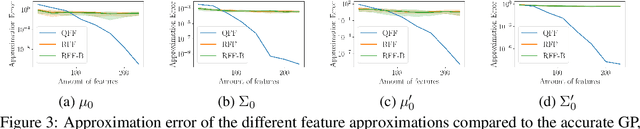
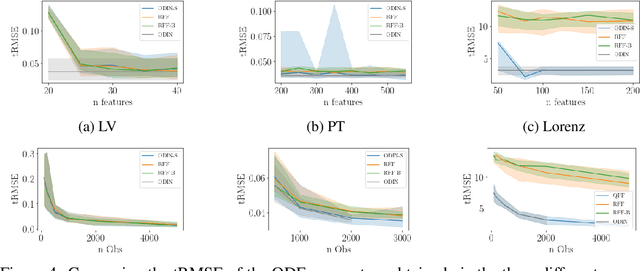
Gaussian processes are an important regression tool with excellent analytic properties which allow for direct integration of derivative observations. However, vanilla GP methods scale cubically in the amount of observations. In this work, we propose a novel approach for scaling GP regression with derivatives based on quadrature Fourier features. We then prove deterministic, non-asymptotic and exponentially fast decaying error bounds which apply for both the approximated kernel as well as the approximated posterior. To furthermore illustrate the practical applicability of our method, we then apply it to ODIN, a recently developed algorithm for ODE parameter inference. In an extensive experiments section, all results are empirically validated, demonstrating the speed, accuracy, and practical applicability of this approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge