Doubly Robust Structure Identification from Temporal Data

Learning the causes of time-series data is a fundamental task in many applications, spanning from finance to earth sciences or bio-medical applications. Common approaches for this task are based on vector auto-regression, and they do not take into account unknown confounding between potential causes. However, in settings with many potential causes and noisy data, these approaches may be substantially biased. Furthermore, potential causes may be correlated in practical applications. Moreover, existing algorithms often do not work with cyclic data. To address these challenges, we propose a new doubly robust method for Structure Identification from Temporal Data ( SITD ). We provide theoretical guarantees, showing that our method asymptotically recovers the true underlying causal structure. Our analysis extends to cases where the potential causes have cycles and they may be confounded. We further perform extensive experiments to showcase the superior performance of our method.

SLEIPNIR: Deterministic and Provably Accurate Feature Expansion for Gaussian Process Regression with Derivatives

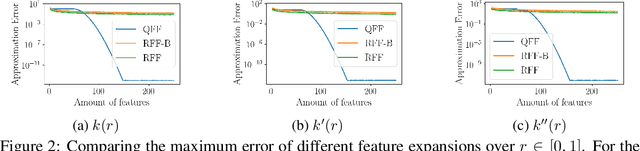
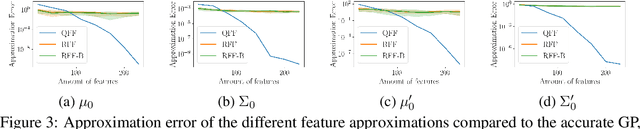
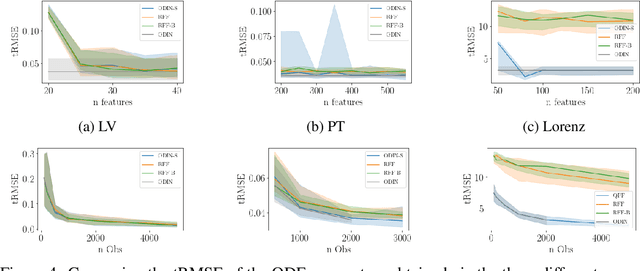
Gaussian processes are an important regression tool with excellent analytic properties which allow for direct integration of derivative observations. However, vanilla GP methods scale cubically in the amount of observations. In this work, we propose a novel approach for scaling GP regression with derivatives based on quadrature Fourier features. We then prove deterministic, non-asymptotic and exponentially fast decaying error bounds which apply for both the approximated kernel as well as the approximated posterior. To furthermore illustrate the practical applicability of our method, we then apply it to ODIN, a recently developed algorithm for ODE parameter inference. In an extensive experiments section, all results are empirically validated, demonstrating the speed, accuracy, and practical applicability of this approach.