Challenges and Opportunities in High-dimensional Variational Inference

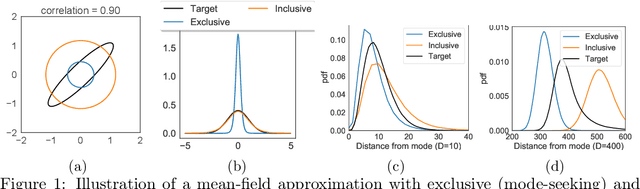
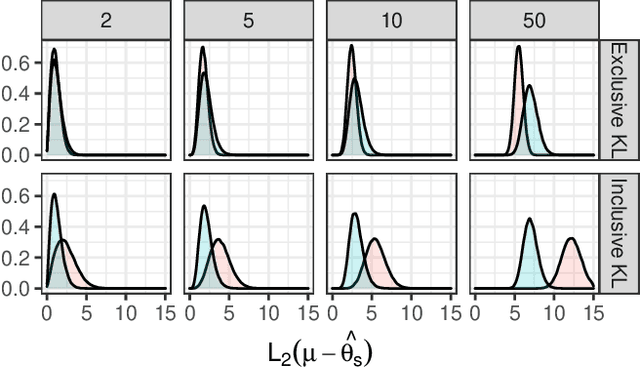
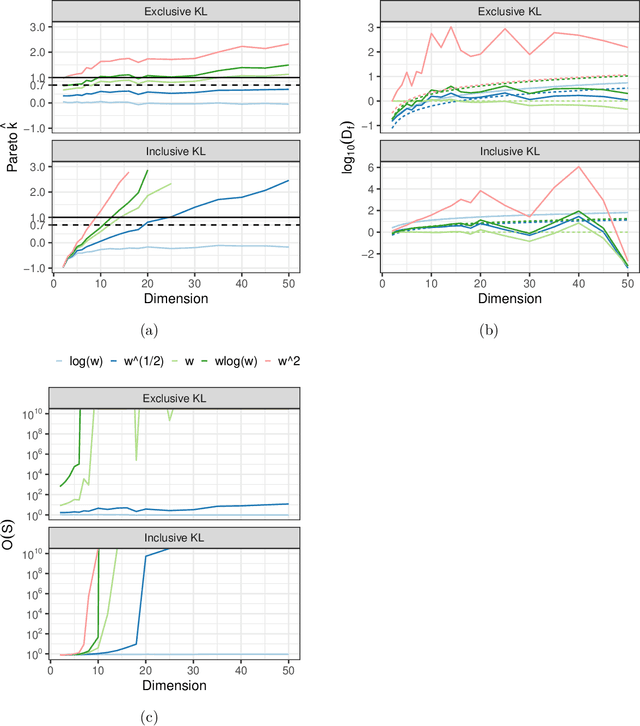
We explore the limitations of and best practices for using black-box variational inference to estimate posterior summaries of the model parameters. By taking an importance sampling perspective, we are able to explain and empirically demonstrate: 1) why the intuitions about the behavior of approximate families and divergences for low-dimensional posteriors fail for higher-dimensional posteriors, 2) how we can diagnose the pre-asymptotic reliability of variational inference in practice by examining the behavior of the density ratios (i.e., importance weights), 3) why the choice of variational objective is not as relevant for higher-dimensional posteriors, and 4) why, although flexible variational families can provide some benefits in higher dimensions, they also introduce additional optimization challenges. Based on these findings, for high-dimensional posteriors we recommend using the exclusive KL divergence that is most stable and easiest to optimize, and then focusing on improving the variational family or using model parameter transformations to make the posterior more similar to the approximating family. Our results also show that in low to moderate dimensions, heavy-tailed variational families and mass-covering divergences can increase the chances that the approximation can be improved by importance sampling.

Robust, Accurate Stochastic Optimization for Variational Inference

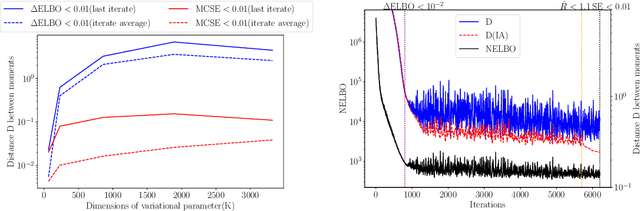
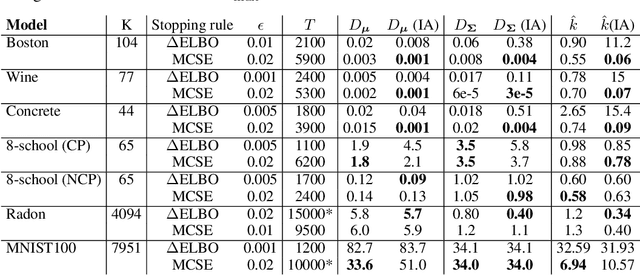
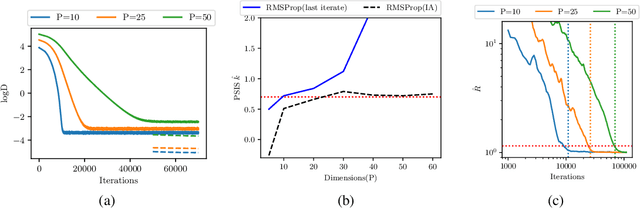
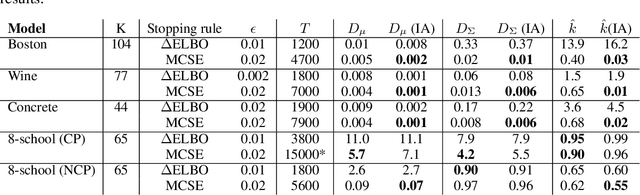
We consider the problem of fitting variational posterior approximations using stochastic optimization methods. The performance of these approximations depends on (1) how well the variational family matches the true posterior distribution,(2) the choice of divergence, and (3) the optimization of the variational objective. We show that even in the best-case scenario when the exact posterior belongs to the assumed variational family, common stochastic optimization methods lead to poor variational approximations if the problem dimension is moderately large. We also demonstrate that these methods are not robust across diverse model types. Motivated by these findings, we develop a more robust and accurate stochastic optimization framework by viewing the underlying optimization algorithm as producing a Markov chain. Our approach is theoretically motivated and includes a diagnostic for convergence and a novel stopping rule, both of which are robust to noisy evaluations of the objective function. We show empirically that the proposed framework works well on a diverse set of models: it can automatically detect stochastic optimization failure or inaccurate variational approximation

Group Heterogeneity Assessment for Multilevel Models

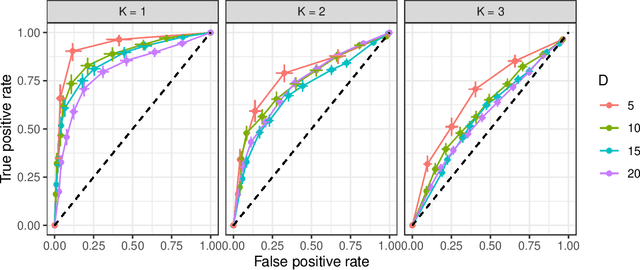
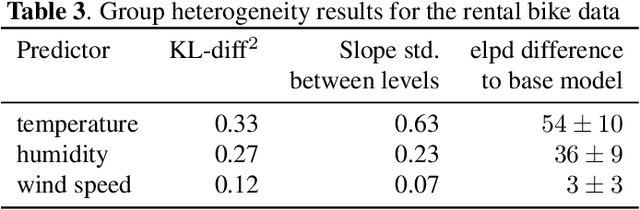
Many data sets contain an inherent multilevel structure, for example, because of repeated measurements of the same observational units. Taking this structure into account is critical for the accuracy and calibration of any statistical analysis performed on such data. However, the large number of possible model configurations hinders the use of multilevel models in practice. In this work, we propose a flexible framework for efficiently assessing differences between the levels of given grouping variables in the data. The assessed group heterogeneity is valuable in choosing the relevant group coefficients to consider in a multilevel model. Our empirical evaluations demonstrate that the framework can reliably identify relevant multilevel components in both simulated and real data sets.