The Cambridge Law Corpus: A Corpus for Legal AI Research

We introduce the Cambridge Law Corpus (CLC), a corpus for legal AI research. It consists of over 250 000 court cases from the UK. Most cases are from the 21st century, but the corpus includes cases as old as the 16th century. This paper presents the first release of the corpus, containing the raw text and meta-data. Together with the corpus, we provide annotations on case outcomes for 638 cases, done by legal experts. Using our annotated data, we have trained and evaluated case outcome extraction with GPT-3, GPT-4 and RoBERTa models to provide benchmarks. We include an extensive legal and ethical discussion to address the potentially sensitive nature of this material. As a consequence, the corpus will only be released for research purposes under certain restrictions.

Probabilistic Embeddings with Laplacian Graph Priors

We introduce probabilistic embeddings using Laplacian priors (PELP). The proposed model enables incorporating graph side-information into static word embeddings. We theoretically show that the model unifies several previously proposed embedding methods under one umbrella. PELP generalises graph-enhanced, group, dynamic, and cross-lingual static word embeddings. PELP also enables any combination of these previous models in a straightforward fashion. Furthermore, we empirically show that our model matches the performance of previous models as special cases. In addition, we demonstrate its flexibility by applying it to the comparison of political sociolects over time. Finally, we provide code as a TensorFlow implementation enabling flexible estimation in different settings.

Robust, Accurate Stochastic Optimization for Variational Inference

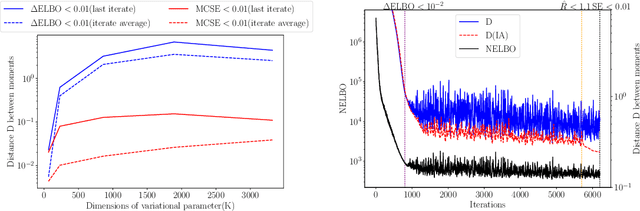
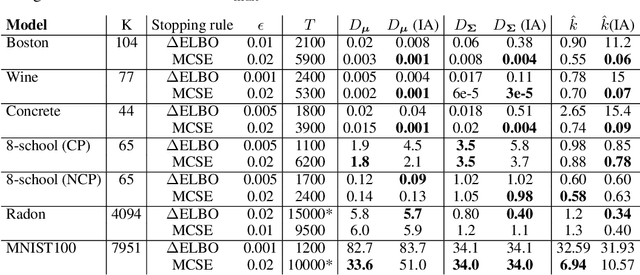
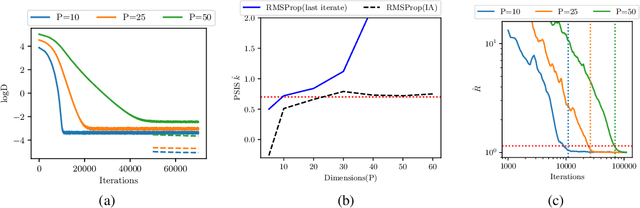
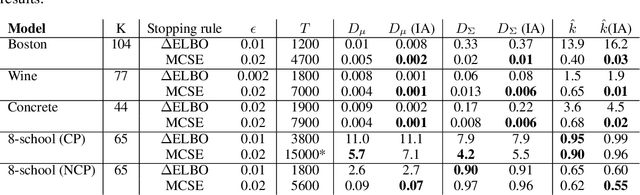
We consider the problem of fitting variational posterior approximations using stochastic optimization methods. The performance of these approximations depends on (1) how well the variational family matches the true posterior distribution,(2) the choice of divergence, and (3) the optimization of the variational objective. We show that even in the best-case scenario when the exact posterior belongs to the assumed variational family, common stochastic optimization methods lead to poor variational approximations if the problem dimension is moderately large. We also demonstrate that these methods are not robust across diverse model types. Motivated by these findings, we develop a more robust and accurate stochastic optimization framework by viewing the underlying optimization algorithm as producing a Markov chain. Our approach is theoretically motivated and includes a diagnostic for convergence and a novel stopping rule, both of which are robust to noisy evaluations of the objective function. We show empirically that the proposed framework works well on a diverse set of models: it can automatically detect stochastic optimization failure or inaccurate variational approximation

Interpretable Word Embeddings via Informative Priors

Word embeddings have demonstrated strong performance on NLP tasks. However, lack of interpretability and the unsupervised nature of word embeddings have limited their use within computational social science and digital humanities. We propose the use of informative priors to create interpretable and domain-informed dimensions for probabilistic word embeddings. Experimental results show that sensible priors can capture latent semantic concepts better than or on-par with the current state of the art, while retaining the simplicity and generalizability of using priors.

Sparse Parallel Training of Hierarchical Dirichlet Process Topic Models

Nonparametric extensions of topic models such as Latent Dirichlet Allocation, including Hierarchical Dirichlet Process (HDP), are often studied in natural language processing. Training these models generally requires use of serial algorithms, which limits scalability to large data sets and complicates acceleration via use of parallel and distributed systems. Most current approaches to scalable training of such models either don't converge to the correct target, or are not data-parallel. Moreover, these approaches generally do not utilize all available sources of sparsity found in natural language - an important way to make computation efficient. Based upon a representation of certain conditional distributions within an HDP, we propose a doubly sparse data-parallel sampler for the HDP topic model that addresses these issues. We benchmark our method on a well-known corpora (PubMed) with 8m documents and 768m tokens, using a single multi-core machine in under three days.

Bayesian leave-one-out cross-validation for large data

Model inference, such as model comparison, model checking, and model selection, is an important part of model development. Leave-one-out cross-validation (LOO) is a general approach for assessing the generalizability of a model, but unfortunately, LOO does not scale well to large datasets. We propose a combination of using approximate inference techniques and probability-proportional-to-size-sampling (PPS) for fast LOO model evaluation for large datasets. We provide both theoretical and empirical results showing good properties for large data.

Polya Urn Latent Dirichlet Allocation: a doubly sparse massively parallel sampler

Latent Dirichlet Allocation (LDA) is a topic model widely used in natural language processing and machine learning. Most approaches to training the model rely on iterative algorithms, which makes it difficult to run LDA on big corpora that are best analyzed in parallel and distributed computational environments. Indeed, current approaches to parallel inference either don't converge to the correct posterior or require storage of large dense matrices in memory. We present a novel sampler that overcomes both problems, and we show that this sampler is faster, both empirically and theoretically, than previous Gibbs samplers for LDA. We do so by employing a novel P\'olya-urn-based approximation in the sparse partially collapsed sampler for LDA. We prove that the approximation error vanishes with data size, making our algorithm asymptotically exact, a property of importance for large-scale topic models. In addition, we show, via an explicit example, that -- contrary to popular belief in the topic modeling literature -- partially collapsed samplers can be more efficient than fully collapsed samplers. We conclude by comparing the performance of our algorithm with that of other approaches on well-known corpora.

Sparse Partially Collapsed MCMC for Parallel Inference in Topic Models

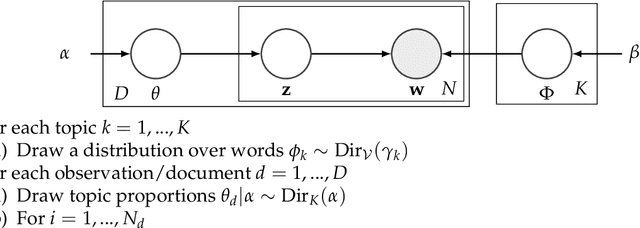
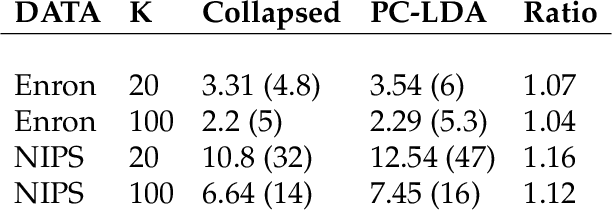
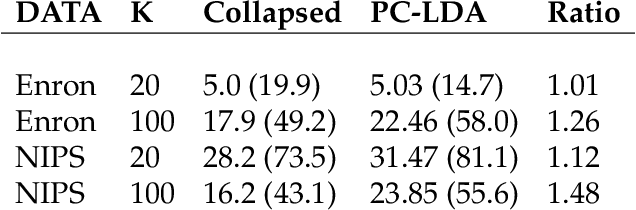
Topic models, and more specifically the class of Latent Dirichlet Allocation (LDA), are widely used for probabilistic modeling of text. MCMC sampling from the posterior distribution is typically performed using a collapsed Gibbs sampler. We propose a parallel sparse partially collapsed Gibbs sampler and compare its speed and efficiency to state-of-the-art samplers for topic models on five well-known text corpora of differing sizes and properties. In particular, we propose and compare two different strategies for sampling the parameter block with latent topic indicators. The experiments show that the increase in statistical inefficiency from only partial collapsing is smaller than commonly assumed, and can be more than compensated by the speedup from parallelization and sparsity on larger corpora. We also prove that the partially collapsed samplers scale well with the size of the corpus. The proposed algorithm is fast, efficient, exact, and can be used in more modeling situations than the ordinary collapsed sampler.

DOLDA - a regularized supervised topic model for high-dimensional multi-class regression

Generating user interpretable multi-class predictions in data rich environments with many classes and explanatory covariates is a daunting task. We introduce Diagonal Orthant Latent Dirichlet Allocation (DOLDA), a supervised topic model for multi-class classification that can handle both many classes as well as many covariates. To handle many classes we use the recently proposed Diagonal Orthant (DO) probit model (Johndrow et al., 2013) together with an efficient Horseshoe prior for variable selection/shrinkage (Carvalho et al., 2010). We propose a computationally efficient parallel Gibbs sampler for the new model. An important advantage of DOLDA is that learned topics are directly connected to individual classes without the need for a reference class. We evaluate the model's predictive accuracy on two datasets and demonstrate DOLDA's advantage in interpreting the generated predictions.