Variational Quantum Optimization with Continuous Bandits

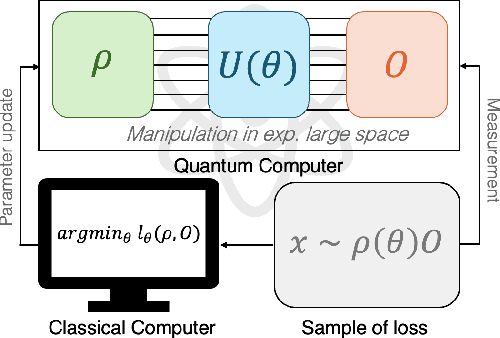
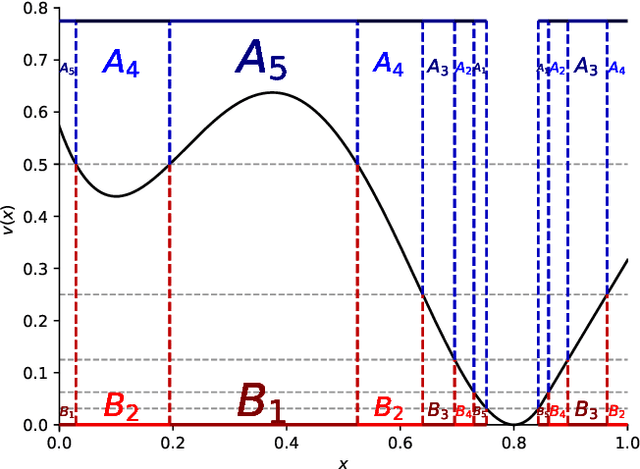
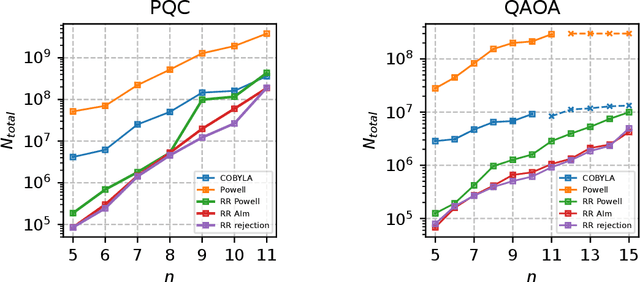
We introduce a novel approach to variational Quantum algorithms (VQA) via continuous bandits. VQA are a class of hybrid Quantum-classical algorithms where the parameters of Quantum circuits are optimized by classical algorithms. Previous work has used zero and first order gradient based methods, however such algorithms suffer from the barren plateau (BP) problem where gradients and loss differences are exponentially small. We introduce an approach using bandits methods which combine global exploration with local exploitation. We show how VQA can be formulated as a best arm identification problem in a continuous space of arms with Lipschitz smoothness. While regret minimization has been addressed in this setting, existing methods for pure exploration only cover discrete spaces. We give the first results for pure exploration in a continuous setting and derive a fixed-confidence, information-theoretic, instance specific lower bound. Under certain assumptions on the expected payoff, we derive a simple algorithm, which is near-optimal with respect to our lower bound. Finally, we apply our continuous bandit algorithm to two VQA schemes: a PQC and a QAOA quantum circuit, showing that we significantly outperform the previously known state of the art methods (which used gradient based methods).

Noise Sensitivity and Stability of Deep Neural Networks for Binary Classification

A first step is taken towards understanding often observed non-robustness phenomena of deep neural net (DNN) classifiers. This is done from the perspective of Boolean functions by asking if certain sequences of Boolean functions represented by common DNN models are noise sensitive or noise stable, concepts defined in the Boolean function literature. Due to the natural randomness in DNN models, these concepts are extended to annealed and quenched versions. Here we sort out the relation between these definitions and investigate the properties of two standard DNN architectures, the fully connected and convolutional models, when initiated with Gaussian weights.

Robust Neural Network Classification via Double Regularization

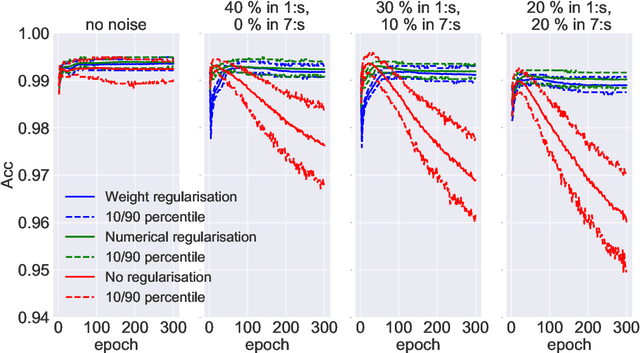
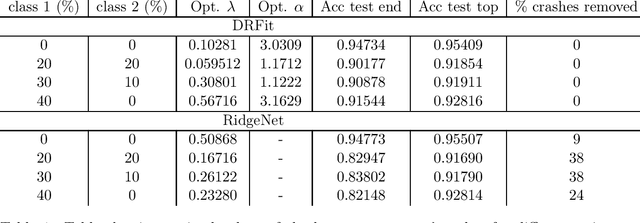
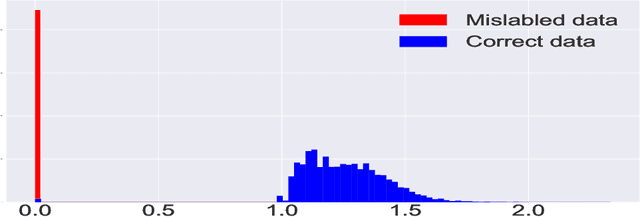
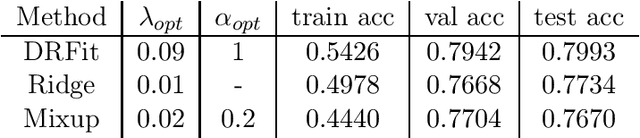
The presence of mislabeled observations in data is a notoriously challenging problem in statistics and machine learning, associated with poor generalization properties for both traditional classifiers and, perhaps even more so, flexible classifiers like neural networks. Here we propose a novel double regularization of the neural network training loss that combines a penalty on the complexity of the classification model and an optimal reweighting of training observations. The combined penalties result in improved generalization properties and strong robustness against overfitting in different settings of mislabeled training data and also against variation in initial parameter values when training. We provide a theoretical justification for our proposed method derived for a simple case of logistic regression. We demonstrate the double regularization model, here denoted by DRFit, for neural net classification of (i) MNIST and (ii) CIFAR-10, in both cases with simulated mislabeling. We also illustrate that DRFit identifies mislabeled data points with very good precision. This provides strong support for DRFit as a practical of-the-shelf classifier, since, without any sacrifice in performance, we get a classifier that simultaneously reduces overfitting against mislabeling and gives an accurate measure of the trustworthiness of the labels.

Bayesian leave-one-out cross-validation for large data

Model inference, such as model comparison, model checking, and model selection, is an important part of model development. Leave-one-out cross-validation (LOO) is a general approach for assessing the generalizability of a model, but unfortunately, LOO does not scale well to large datasets. We propose a combination of using approximate inference techniques and probability-proportional-to-size-sampling (PPS) for fast LOO model evaluation for large datasets. We provide both theoretical and empirical results showing good properties for large data.

Fast mixing for Latent Dirichlet allocation

Markov chain Monte Carlo (MCMC) algorithms are ubiquitous in probability theory in general and in machine learning in particular. A Markov chain is devised so that its stationary distribution is some probability distribution of interest. Then one samples from the given distribution by running the Markov chain for a "long time" until it appears to be stationary and then collects the sample. However these chains are often very complex and there are no theoretical guarantees that stationarity is actually reached. In this paper we study the Gibbs sampler of the posterior distribution of a very simple case of Latent Dirichlet Allocation, the arguably most well known Bayesian unsupervised learning model for text generation and text classification. It is shown that when the corpus consists of two long documents of equal length $m$ and the vocabulary consists of only two different words, the mixing time is at most of order $m^2\log m$ (which corresponds to $m\log m$ rounds over the corpus). It will be apparent from our analysis that it seems very likely that the mixing time is not much worse in the more relevant case when the number of documents and the size of the vocabulary are also large as long as each word is represented a large number in each document, even though the computations involved may be intractable.