Variational Quantum Optimization with Continuous Bandits

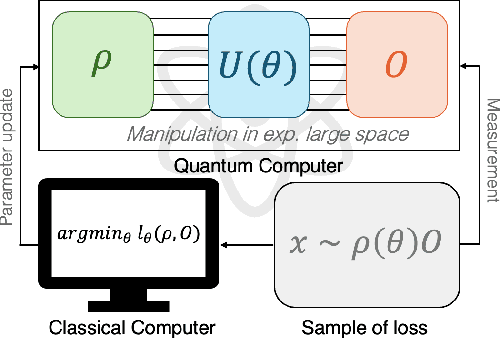
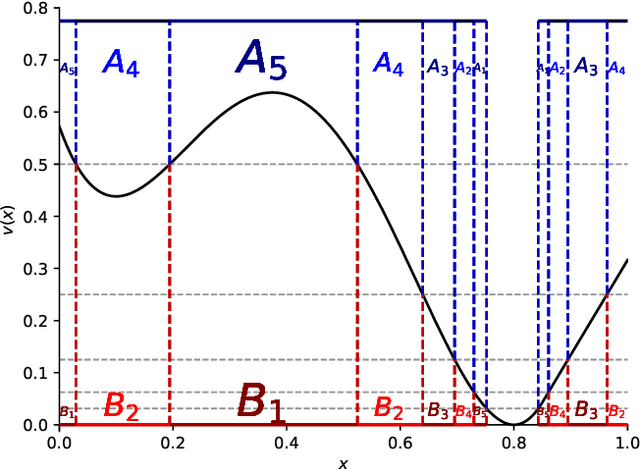
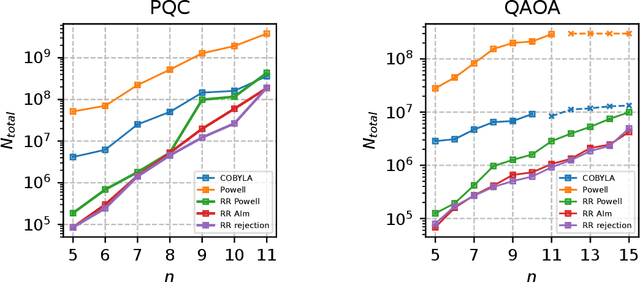
We introduce a novel approach to variational Quantum algorithms (VQA) via continuous bandits. VQA are a class of hybrid Quantum-classical algorithms where the parameters of Quantum circuits are optimized by classical algorithms. Previous work has used zero and first order gradient based methods, however such algorithms suffer from the barren plateau (BP) problem where gradients and loss differences are exponentially small. We introduce an approach using bandits methods which combine global exploration with local exploitation. We show how VQA can be formulated as a best arm identification problem in a continuous space of arms with Lipschitz smoothness. While regret minimization has been addressed in this setting, existing methods for pure exploration only cover discrete spaces. We give the first results for pure exploration in a continuous setting and derive a fixed-confidence, information-theoretic, instance specific lower bound. Under certain assumptions on the expected payoff, we derive a simple algorithm, which is near-optimal with respect to our lower bound. Finally, we apply our continuous bandit algorithm to two VQA schemes: a PQC and a QAOA quantum circuit, showing that we significantly outperform the previously known state of the art methods (which used gradient based methods).

ACE: Abstractions for Communicating Efficiently

A central but unresolved aspect of problem-solving in AI is the capability to introduce and use abstractions, something humans excel at. Work in cognitive science has demonstrated that humans tend towards higher levels of abstraction when engaged in collaborative task-oriented communication, enabling gradually shorter and more information-efficient utterances. Several computational methods have attempted to replicate this phenomenon, but all make unrealistic simplifying assumptions about how abstractions are introduced and learned. Our method, Abstractions for Communicating Efficiently (ACE), overcomes these limitations through a neuro-symbolic approach. On the symbolic side, we draw on work from library learning for proposing abstractions. We combine this with neural methods for communication and reinforcement learning, via a novel use of bandit algorithms for controlling the exploration and exploitation trade-off in introducing new abstractions. ACE exhibits similar tendencies to humans on a collaborative construction task from the cognitive science literature, where one agent (the architect) instructs the other (the builder) to reconstruct a scene of block-buildings. ACE results in the emergence of an efficient language as a by-product of collaborative communication. Beyond providing mechanistic insights into human communication, our work serves as a first step to providing conversational agents with the ability for human-like communicative abstractions.

Learning Efficient Recursive Numeral Systems via Reinforcement Learning

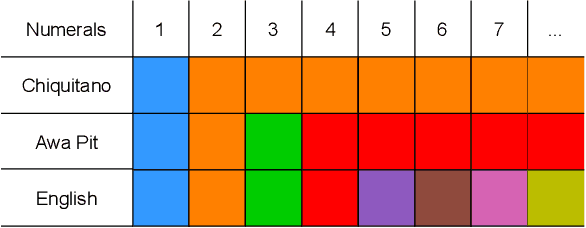
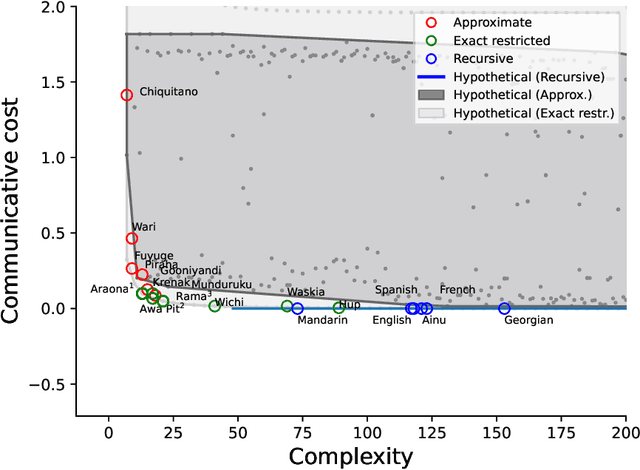
The emergence of mathematical concepts, such as number systems, is an understudied area in AI for mathematics and reasoning. It has previously been shown Carlsson et al. (2021) that by using reinforcement learning (RL), agents can derive simple approximate and exact-restricted numeral systems. However, it is a major challenge to show how more complex recursive numeral systems, similar to the one utilised in English, could arise via a simple learning mechanism such as RL. Here, we introduce an approach towards deriving a mechanistic explanation of the emergence of recursive number systems where we consider an RL agent which directly optimizes a lexicon under a given meta-grammar. Utilising a slightly modified version of the seminal meta-grammar of Hurford (1975), we demonstrate that our RL agent can effectively modify the lexicon towards Pareto-optimal configurations which are comparable to those observed within human numeral systems.

Predicting Ground State Properties: Constant Sample Complexity and Deep Learning Algorithms

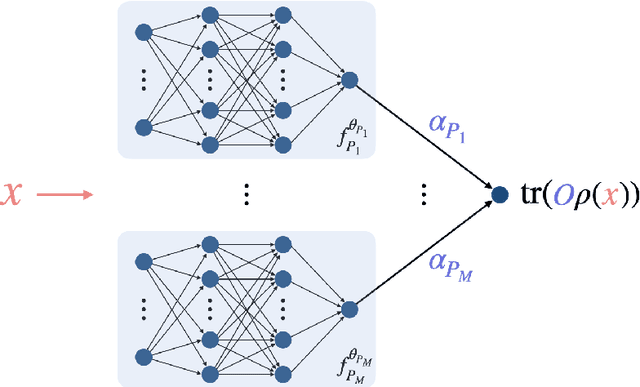
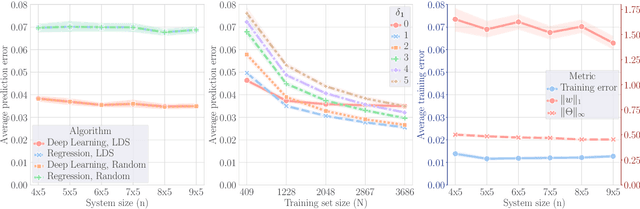
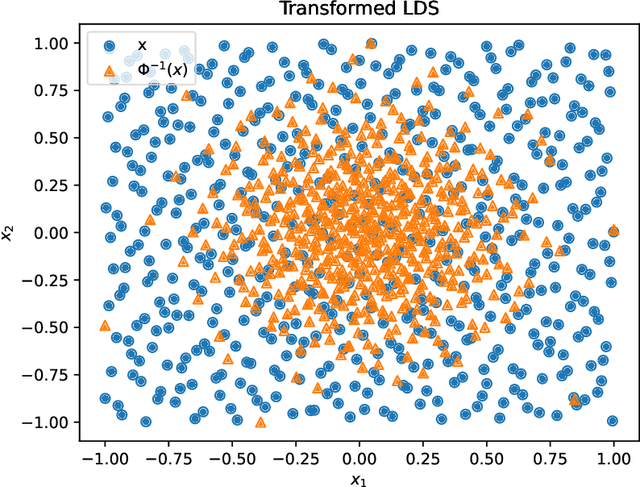
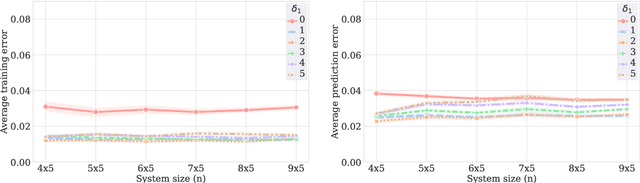
A fundamental problem in quantum many-body physics is that of finding ground states of local Hamiltonians. A number of recent works gave provably efficient machine learning (ML) algorithms for learning ground states. Specifically, [Huang et al. Science 2022], introduced an approach for learning properties of the ground state of an $n$-qubit gapped local Hamiltonian $H$ from only $n^{\mathcal{O}(1)}$ data points sampled from Hamiltonians in the same phase of matter. This was subsequently improved by [Lewis et al. Nature Communications 2024], to $\mathcal{O}(\log n)$ samples when the geometry of the $n$-qubit system is known. In this work, we introduce two approaches that achieve a constant sample complexity, independent of system size $n$, for learning ground state properties. Our first algorithm consists of a simple modification of the ML model used by Lewis et al. and applies to a property of interest known beforehand. Our second algorithm, which applies even if a description of the property is not known, is a deep neural network model. While empirical results showing the performance of neural networks have been demonstrated, to our knowledge, this is the first rigorous sample complexity bound on a neural network model for predicting ground state properties. We also perform numerical experiments that confirm the improved scaling of our approach compared to earlier results.

Active Preference Learning for Ordering Items In- and Out-of-sample

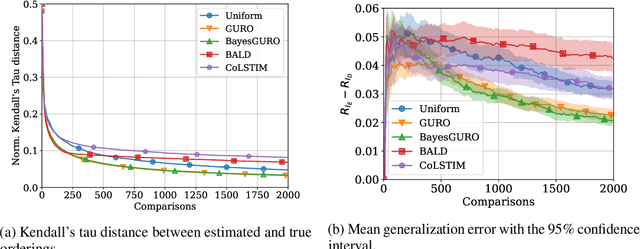
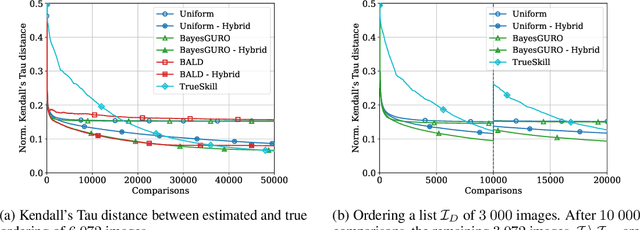
Learning an ordering of items based on noisy pairwise comparisons is useful when item-specific labels are difficult to assign, for example, when annotators have to make subjective assessments. Algorithms have been proposed for actively sampling comparisons of items to minimize the number of annotations necessary for learning an accurate ordering. However, many ignore shared structure between items, treating them as unrelated, limiting sample efficiency and precluding generalization to new items. In this work, we study active learning with pairwise preference feedback for ordering items with contextual attributes, both in- and out-of-sample. We give an upper bound on the expected ordering error incurred by active learning strategies under a logistic preference model, in terms of the aleatoric and epistemic uncertainty in comparisons, and propose two algorithms designed to greedily minimize this bound. We evaluate these algorithms in two realistic image ordering tasks, including one with comparisons made by human annotators, and demonstrate superior sample efficiency compared to non-contextual ranking approaches and active preference learning baselines.

Pure Exploration in Bandits with Linear Constraints

We address the problem of identifying the optimal policy with a fixed confidence level in a multi-armed bandit setup, when \emph{the arms are subject to linear constraints}. Unlike the standard best-arm identification problem which is well studied, the optimal policy in this case may not be deterministic and could mix between several arms. This changes the geometry of the problem which we characterize via an information-theoretic lower bound. We introduce two asymptotically optimal algorithms for this setting, one based on the Track-and-Stop method and the other based on a game-theoretic approach. Both these algorithms try to track an optimal allocation based on the lower bound and computed by a weighted projection onto the boundary of a normal cone. Finally, we provide empirical results that validate our bounds and visualize how constraints change the hardness of the problem.

Pragmatic Reasoning in Structured Signaling Games

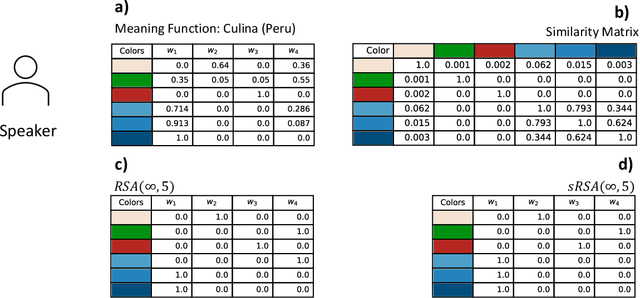
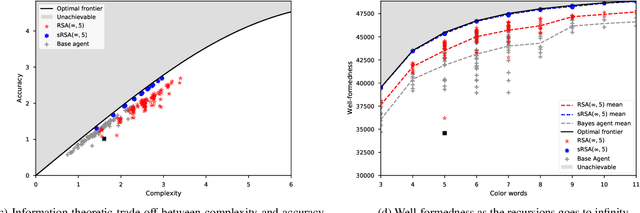
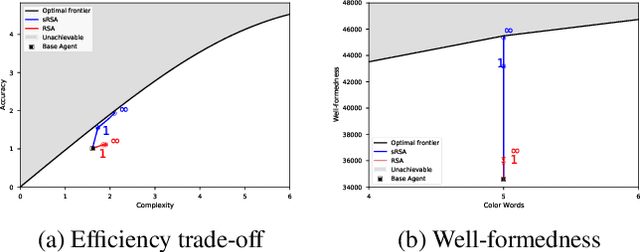
In this work we introduce a structured signaling game, an extension of the classical signaling game with a similarity structure between meanings in the context, along with a variant of the Rational Speech Act (RSA) framework which we call structured-RSA (sRSA) for pragmatic reasoning in structured domains. We explore the behavior of the sRSA in the domain of color and show that pragmatic agents using sRSA on top of semantic representations, derived from the World Color Survey, attain efficiency very close to the information theoretic limit after only 1 or 2 levels of recursion. We also explore the interaction between pragmatic reasoning and learning in multi-agent reinforcement learning framework. Our results illustrate that artificial agents using sRSA develop communication closer to the information theoretic frontier compared to agents using RSA and just reinforcement learning. We also find that the ambiguity of the semantic representation increases as the pragmatic agents are allowed to perform deeper reasoning about each other during learning.

Iterated learning and communication jointly explain efficient color naming systems

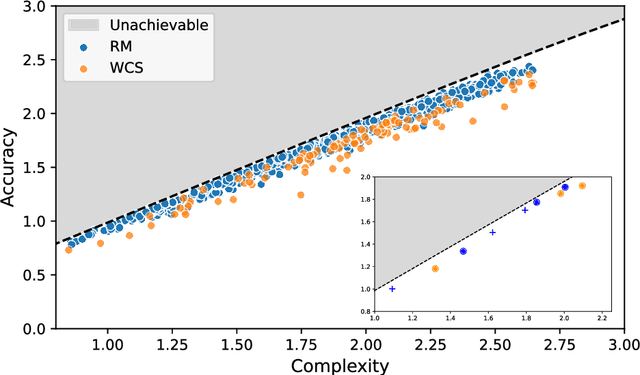
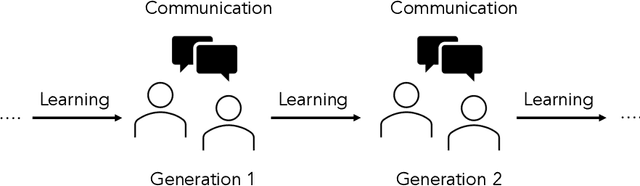
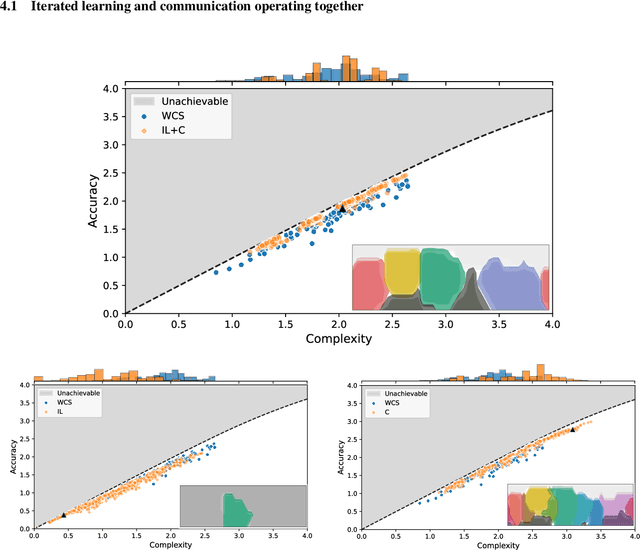
It has been argued that semantic systems reflect pressure for efficiency, and a current debate concerns the cultural evolutionary process that produces this pattern. We consider efficiency as instantiated in the Information Bottleneck (IB) principle, and a model of cultural evolution that combines iterated learning and communication. We show that this model, instantiated in neural networks, converges to color naming systems that are efficient in the IB sense and similar to human color naming systems. We also show that iterated learning alone, and communication alone, do not yield the same outcome as clearly.

Thompson Sampling for Bandits with Clustered Arms

We propose algorithms based on a multi-level Thompson sampling scheme, for the stochastic multi-armed bandit and its contextual variant with linear expected rewards, in the setting where arms are clustered. We show, both theoretically and empirically, how exploiting a given cluster structure can significantly improve the regret and computational cost compared to using standard Thompson sampling. In the case of the stochastic multi-armed bandit we give upper bounds on the expected cumulative regret showing how it depends on the quality of the clustering. Finally, we perform an empirical evaluation showing that our algorithms perform well compared to previously proposed algorithms for bandits with clustered arms.

Learning Approximate and Exact Numeral Systems via Reinforcement Learning

Recent work (Xu et al., 2020) has suggested that numeral systems in different languages are shaped by a functional need for efficient communication in an information-theoretic sense. Here we take a learning-theoretic approach and show how efficient communication emerges via reinforcement learning. In our framework, two artificial agents play a Lewis signaling game where the goal is to convey a numeral concept. The agents gradually learn to communicate using reinforcement learning and the resulting numeral systems are shown to be efficient in the information-theoretic framework of Regier et al. (2015); Gibson et al. (2017). They are also shown to be similar to human numeral systems of same type. Our results thus provide a mechanistic explanation via reinforcement learning of the recent results in Xu et al. (2020) and can potentially be generalized to other semantic domains.