Learning Efficient Recursive Numeral Systems via Reinforcement Learning
Paper and Code
Sep 11, 2024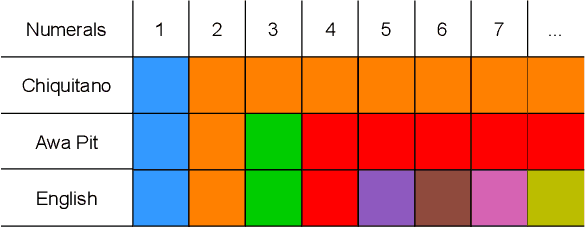

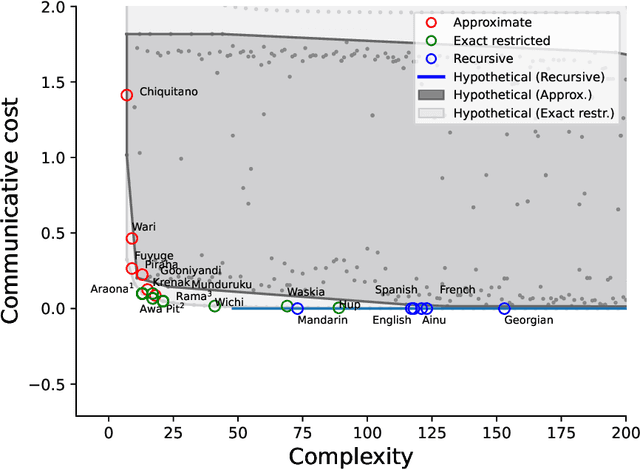

The emergence of mathematical concepts, such as number systems, is an understudied area in AI for mathematics and reasoning. It has previously been shown Carlsson et al. (2021) that by using reinforcement learning (RL), agents can derive simple approximate and exact-restricted numeral systems. However, it is a major challenge to show how more complex recursive numeral systems, similar to the one utilised in English, could arise via a simple learning mechanism such as RL. Here, we introduce an approach towards deriving a mechanistic explanation of the emergence of recursive number systems where we consider an RL agent which directly optimizes a lexicon under a given meta-grammar. Utilising a slightly modified version of the seminal meta-grammar of Hurford (1975), we demonstrate that our RL agent can effectively modify the lexicon towards Pareto-optimal configurations which are comparable to those observed within human numeral systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge