ACE: Abstractions for Communicating Efficiently

A central but unresolved aspect of problem-solving in AI is the capability to introduce and use abstractions, something humans excel at. Work in cognitive science has demonstrated that humans tend towards higher levels of abstraction when engaged in collaborative task-oriented communication, enabling gradually shorter and more information-efficient utterances. Several computational methods have attempted to replicate this phenomenon, but all make unrealistic simplifying assumptions about how abstractions are introduced and learned. Our method, Abstractions for Communicating Efficiently (ACE), overcomes these limitations through a neuro-symbolic approach. On the symbolic side, we draw on work from library learning for proposing abstractions. We combine this with neural methods for communication and reinforcement learning, via a novel use of bandit algorithms for controlling the exploration and exploitation trade-off in introducing new abstractions. ACE exhibits similar tendencies to humans on a collaborative construction task from the cognitive science literature, where one agent (the architect) instructs the other (the builder) to reconstruct a scene of block-buildings. ACE results in the emergence of an efficient language as a by-product of collaborative communication. Beyond providing mechanistic insights into human communication, our work serves as a first step to providing conversational agents with the ability for human-like communicative abstractions.

Learning Efficient Recursive Numeral Systems via Reinforcement Learning

The emergence of mathematical concepts, such as number systems, is an understudied area in AI for mathematics and reasoning. It has previously been shown Carlsson et al. (2021) that by using reinforcement learning (RL), agents can derive simple approximate and exact-restricted numeral systems. However, it is a major challenge to show how more complex recursive numeral systems, similar to the one utilised in English, could arise via a simple learning mechanism such as RL. Here, we introduce an approach towards deriving a mechanistic explanation of the emergence of recursive number systems where we consider an RL agent which directly optimizes a lexicon under a given meta-grammar. Utilising a slightly modified version of the seminal meta-grammar of Hurford (1975), we demonstrate that our RL agent can effectively modify the lexicon towards Pareto-optimal configurations which are comparable to those observed within human numeral systems.

An Intrusion Response System utilizing Deep Q-Networks and System Partitions

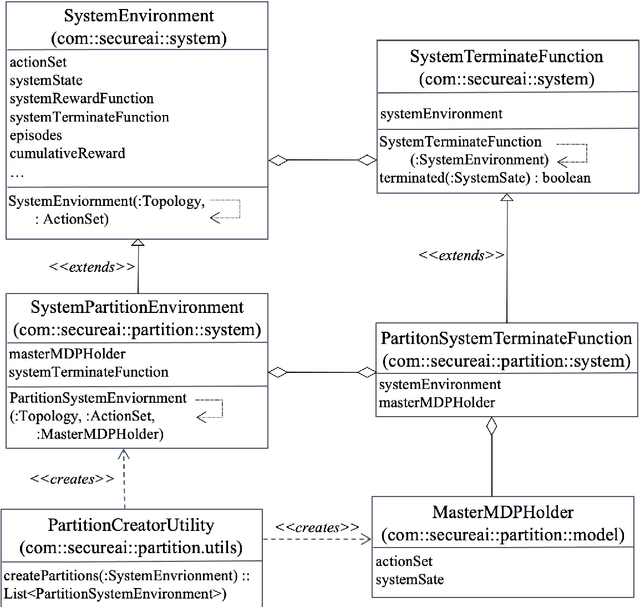
Intrusion Response is a relatively new field of research. Recent approaches for the creation of Intrusion Response Systems (IRSs) use Reinforcement Learning (RL) as a primary technique for the optimal or near-optimal selection of the proper countermeasure to take in order to stop or mitigate an ongoing attack. However, most of them do not consider the fact that systems can change over time or, in other words, that systems exhibit a non-stationary behavior. Furthermore, stateful approaches, such as those based on RL, suffer the curse of dimensionality, due to a state space growing exponentially with the size of the protected system. In this paper, we introduce and develop an IRS software prototype, named irs-partition. It leverages the partitioning of the protected system and Deep Q-Networks to address the curse of dimensionality by supporting a multi-agent formulation. Furthermore, it exploits transfer learning to follow the evolution of non-stationary systems.